题目内容
已知椭圆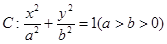 的左右焦点分别是
的左右焦点分别是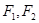 ,离心率
,离心率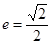 ,
,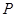 为椭圆上任一点,且
为椭圆上任一点,且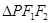 的最大面积为
的最大面积为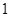 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设斜率为 的直线
的直线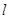 交椭圆
交椭圆 于
于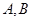 两点,且以
两点,且以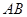 为直径的圆恒过原点
为直径的圆恒过原点 ,若实数
,若实数 满足条件
满足条件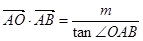 ,求
,求 的最大值.
的最大值.
(Ⅰ)椭圆 的方程
的方程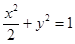 ;(Ⅱ)
;(Ⅱ) 的最大值为
的最大值为 .
.
解析试题分析:(Ⅰ)依题意得: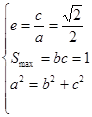 ,这是一个关于
,这是一个关于 的方程组,解这个方程组便可得
的方程组,解这个方程组便可得 的值,从而得椭圆
的值,从而得椭圆 的方程.
的方程.
(Ⅱ)设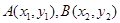 ,由于以
,由于以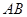 为直径的圆恒过原点
为直径的圆恒过原点 ,所以
,所以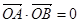 ,即
,即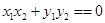 ……………………………………………………①
……………………………………………………①
设直线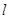 的方程
的方程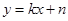 ,联立方程组
,联立方程组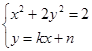 ,再由根与系数的关系可得:
,再由根与系数的关系可得: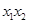 、
、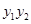 ,代入①便得一个含
,代入①便得一个含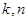 的等式.
的等式.
将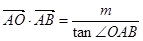 变形化简得:
变形化简得: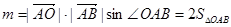 .
.
因此,要求 的最大值,只需求
的最大值,只需求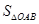 的最大值,而
的最大值,而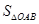 可以用含
可以用含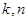 的式子表示出来,再利用前面含
的式子表示出来,再利用前面含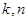 的等式换掉一个变量,得一个只含一个变量的式子,再利用求函数最值的方法,便可求出其最大值.
的等式换掉一个变量,得一个只含一个变量的式子,再利用求函数最值的方法,便可求出其最大值.
试题解析:(Ⅰ)依题意得: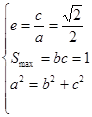 ,解得:
,解得: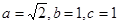 ,
,
于是:椭圆 的方程
的方程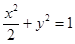 ,
,
(Ⅱ)设直线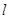 的方程
的方程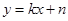 由
由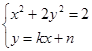 得:
得: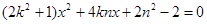 ,
,
设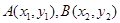 ,则
,则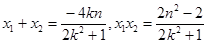 .
.
由于以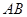 为直径的圆恒过原点
为直径的圆恒过原点 ,于是
,于是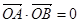 ,即
,即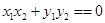 ,
,
又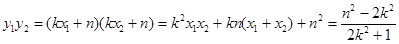 ,
,
于是: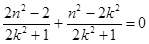 ,即
,即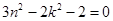
依题意有: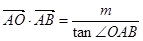 ,即
,即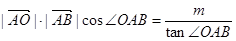 .
.
化简得: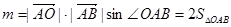 .
.
因此,要求 的最大值,只需求
的最大值,只需求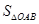 的最大值,下面开始求
的最大值,下面开始求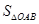 的最大值:
的最大值: 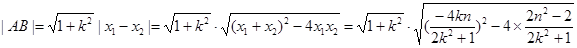
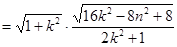 .
.
点 到直线
到直线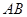 的距离
的距离 ,于是:
,于是: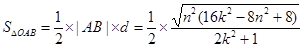 .
.
又因为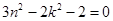 ,所以
,所以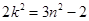 ,
,
代入得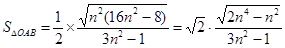 .
.
令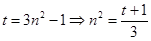 ,
,
于是: .
.
当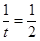 即
即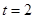 ,即
,即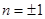 时,
时,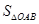 取最大值,且最大值为
取最大值,且最大值为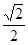 .
.
于是: 的最大值为
的最大值为 .
.
考点:1、椭圆的方程;2、直线与圆锥曲线;3、函数的最值.

练习册系列答案
相关题目
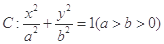 的离心率为
的离心率为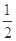 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线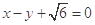 相切,过点P(4,0)且不垂直于x轴直线
相切,过点P(4,0)且不垂直于x轴直线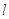 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.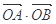 的取值范围;
的取值范围;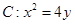 的焦点为
的焦点为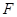 ,过点
,过点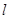 交抛物线
交抛物线 于
于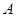 、
、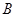 两点,经过
两点,经过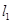 、
、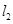 ,切线
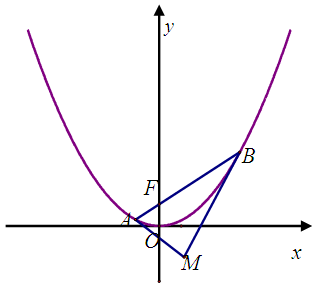
,切线 .
.
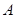 在第二象限,且到准线距离为
在第二象限,且到准线距离为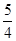 时,求
时,求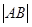 ;
;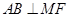 .
. 中,已知圆
中,已知圆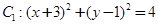 和圆
和圆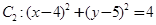 .
. 过点
过点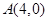 ,且被圆
,且被圆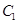 截得的弦长为
截得的弦长为 ,求直线
,求直线 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点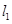 和
和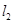 ,它们分别与圆
,它们分别与圆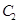 相交,且直线
相交,且直线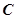 以椭圆
以椭圆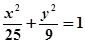 的两个焦点为焦点,且双曲线
的两个焦点为焦点,且双曲线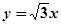 ,
,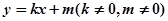 与双曲线
与双曲线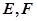 ,且
,且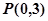 为圆心的圆上,求实数
为圆心的圆上,求实数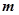 的取值范围.
的取值范围.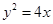 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点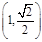 .
.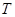
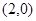 ,过点F2作直线
,过点F2作直线 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且 ,若
,若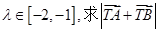 的取值范围.
的取值范围.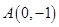 ,焦点在
,焦点在 轴上,若右焦点到直线
轴上,若右焦点到直线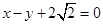 的距离为3.
的距离为3.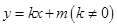 与椭圆相交于不同的两点
与椭圆相交于不同的两点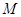 、
、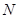 ,当
,当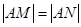 时,求
时,求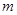 的取值范围.
的取值范围.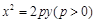 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是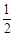 时,
时,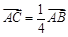 .
.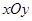 中,
中,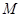 、
、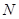 分别是椭圆
分别是椭圆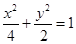 的顶点,过坐标原点的直线交椭圆于
的顶点,过坐标原点的直线交椭圆于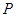 、
、 两点,其中
两点,其中 轴的垂线,垂足为
轴的垂线,垂足为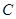 .连接
.连接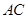 ,并延长交椭圆于点
,并延长交椭圆于点 .设直线
.设直线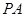 的斜率为
的斜率为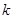 .
.
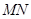 时,求
时,求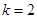 时,求点
时,求点 的距离;
的距离;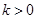 ,求证:
,求证: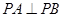 .
.