题目内容
10.已知圆D的半径为1,圆C的方程是(x-2)2+(y+1)2=4,若圆D与圆C相切于点(4,-1),则圆D的标准方程是(x-5)2+(y+1)2=1 或(x-3)2+(y+1)2=1.分析 分两圆外切、内切两种情况,分别求得圆心的坐标,可得要求的圆的方程.
解答 解:圆(x-2)2+(y+1)2=4的圆心为C(2,-1),半径为2,
设所求的圆心坐标为(a,b),
切点为A(4,-1)且半径为1的圆满足$\sqrt{(a-4)^{2}+(b+1)^{2}}=1$,①
(1)若两圆外切,则$\sqrt{(a-2)^{2}+(b+1)^{2}}=1+2=3$,②
由①②得a=5,b=-1,即此时圆心为为M(5,-1),
(2)若两圆内切,则$\sqrt{(a-2)^{2}+(b+1)^{2}}$=2-1=1,③
由①③得a=3,b=-1,即此时圆心为为N(3,-1),
故要求的圆的方程为(x-5)2+(y+1)2=1 或(x-3)2+(y+1)2=1.
点评 本题主要两圆相切的性质,求圆的标准方程,求出圆心的坐标,是解题的关键,注意要分内切和外切两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某人要作一个三角形,要求它的三条高的长度分别是$\frac{1}{13}$,$\frac{1}{11}$,$\frac{1}{5}$,则此人将( )
| A. | 不能作出满足要求的三角形 | B. | 作出一个钝角三角形 | ||
| C. | 作出一个直角三角形 | D. | 作出一个锐角三角形 |
15.在一次某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组)的情况调查中,经统计得到如下2×2列联表:(单位:人)
通过计算得x2=4.852,则参加“篮球小组”与性别间有关系的可能性为( )
(下面临界值表供参考
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
(下面临界值表供参考
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无关系 |
2.函数f(x)=$\frac{1}{2}$tan2x是( )
| A. | 周期为π的偶函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为π的奇函数 |
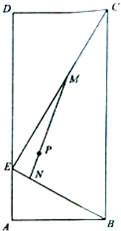 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,