题目内容
8．用数字2，3组成四位数字，则数字2，3至少都出现一次的概率为$\frac{7}{8}$．分析 首先确定数字中2和3的个数，当数字中有1个2，3个3时，当数字中有2个2，2个3时，当数字中有3个2，1个3时，写出每种情况的结果数，最后相加．然后求出基本事件总数，然后求解概率．
解答 解：首先确定数字中2和3 的个数，
当数字中有1个2，3个3时，共有C41=4种结果，
当数字中有2个2，2个3时，共有C42=6种结果，
当数字中有3个2，1个3时，共有有C41=4种结果，
根据分类加法原理知共有4+6+4=14种结果，
全是2，或全是3，各有一个，基本事件总数为16，
用数字2，3组成四位数字，则数字2，3至少都出现一次的概率为：$\frac{14}{16}$=$\frac{7}{8}$．
故答案为：$\frac{7}{8}$．
点评 本题考查分类计数原理，古典概型的概率问题，这种问题一般容易出错，注意分类时要做到不重不漏，本题是一个中档题，也是一个易错题，易错点在数字中重复出现的数字不好处理．
练习册系列答案
相关题目
3．为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
（1）用分层抽样的方法在喜欢打篮球的学生中抽6人，其中男生抽多少人？
（2）在上述抽取的6人中选2人，求恰有一名女生的概率．
（3）为了研究喜欢打蓝球是否与性别有关，由公式K2=$\frac{n（ad-bc）^{2}}{（a+d）（c+d）（a+c）（b+d）}$计算出K2≈8.333，那么你能否有99.5%的把握认为是否喜欢打篮球与性别有关？
附临界值表：
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
（2）在上述抽取的6人中选2人，求恰有一名女生的概率．
（3）为了研究喜欢打蓝球是否与性别有关，由公式K2=$\frac{n（ad-bc）^{2}}{（a+d）（c+d）（a+c）（b+d）}$计算出K2≈8.333，那么你能否有99.5%的把握认为是否喜欢打篮球与性别有关？
附临界值表：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
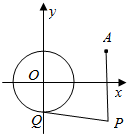如图，已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P向圆O引切线PQ，切点为Q，且有|PQ|=|PA|．