题目内容
18．下图是实数系的结构图，图中1，2，3三个方格中的内容依次为有理数，整数，正整数．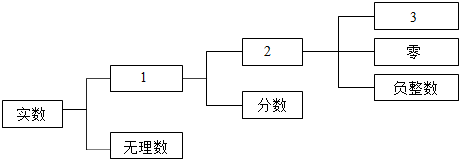
分析 根据中学阶段数系的分类我们易得实数分有理数和无理数，有理数又可以分为分数和整数，而整数又分为正整数，零与负整数，进而得到答案．
解答 解：根据中学阶段数系的分类可得：有理数和无理数统称实数，
分数和整数统称有理数，
负整数、零、正整数统称整数，
可得1，2，3三个方格中的内容分别为有有理数，整数，正整数．
故答案为：有理数，整数，正整数．
点评 本题考查的知识点是结构图，其中熟练掌握数的分类是解答本题的关键．
练习册系列答案
相关题目
6．已知平面区域M={（x，y）|x2+y2≤4}，N={（x，y）|$\left\{\begin{array}{l}{y≥mx+2m}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$}，在区域M上随机取一点A，A落在区域N内的概率为P（N），若P（N）∈[$\frac{1}{2}$，$\frac{3π+2}{4π}$]，则实数m的取值范围是（ ）
| A． | [0，1] | B． | [-$\frac{\sqrt{3}}{3}$，0] | C． | [-1，1] | D． | [-1，0] |
3．
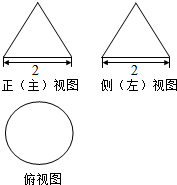已知一个几何体的主视图及左视图均是边长为2的正三角形，俯视图是直径为2的圆，则此几何体的外接球的表面积为（ ）
已知一个几何体的主视图及左视图均是边长为2的正三角形，俯视图是直径为2的圆，则此几何体的外接球的表面积为（ ）| A． | $\frac{4}{3}$π | B． | $\frac{8}{3}$π | C． | $\frac{16}{3}$π | D． | $\frac{32}{3}$π |
8．
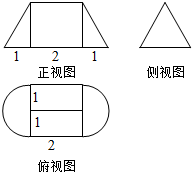一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）
一个几何体的侧视图是边长为2的正三角形，正视图与俯视图的尺寸如图所示，则此几何体的表面积为（ ）| A． | 12+2$\sqrt{3}$+3π | B． | 12+3π | C． | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D． | 2$\sqrt{3}$+$\sqrt{3}$π |