题目内容
16.一中高三年级在一次考试的数学题中,设立了平面几何、极坐标与参数方程的不等式三道选做题,若张明、王小强、李文3名学生必须且只需从中选做一题,且每名学生选做何题相互独立.(1)求张明、王小强、李文3名学生有且只有一人选做平面几何,没有人选做不等式试题的概率;
(2)求这3名学生选做不等式或平面几何题的人数X的分布列及数学期望.
分析 (1)基本事件总数为43,张明、王小强、李文3名学生有且只有一人选做平面几何,没有人选做不等式试题包含的基本事件个数m=${C}_{3}^{2}×2×2$,由此利用等可能事件概率计算公式能求出结果.
(2)不等式或平面几何被这3名学生选做的人数ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 解:(1)设“张明、王小强、李文3名学生有且只有一人选做平面几何,没有人选做不等式试题”为事件A,
则P(A)=$\frac{{C}_{3}^{2}×2×2}{{4}^{3}}$=$\frac{3}{16}$.
答:张明、王小强、李文3名学生有且只有一人选做平面几何,没有人选做不等式试题的概率为$\frac{3}{16}$.
(2)不等式或平面几何被这3名学生选做的人数ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{{2}^{3}}{{4}^{3}}$=$\frac{8}{64}$,
P(ξ=1)=$\frac{{C}_{3}^{1}•{A}_{2}^{1}×{2}^{2}}{{4}^{3}}$=$\frac{24}{64}$,
P(ξ=2)=$\frac{{C}_{3}^{2}{A}_{2}^{1}×2+{C}_{3}^{2}{A}_{2}^{2}×2}{{4}^{3}}$=$\frac{24}{64}$,
P(ξ=3)=$\frac{{C}_{3}^{2}{A}_{2}^{2}+{C}_{3}^{3}{A}_{2}^{1}}{{4}^{3}}$=$\frac{8}{64}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{8}{64}$ | $\frac{24}{64}$ | $\frac{24}{64}$ | $\frac{8}{64}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
6.已知平面区域M={(x,y)|x2+y2≤4},N={(x,y)|$\left\{\begin{array}{l}{y≥mx+2m}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$},在区域M上随机取一点A,A落在区域N内的概率为P(N),若P(N)∈[$\frac{1}{2}$,$\frac{3π+2}{4π}$],则实数m的取值范围是( )
| A. | [0,1] | B. | [-$\frac{\sqrt{3}}{3}$,0] | C. | [-1,1] | D. | [-1,0] |
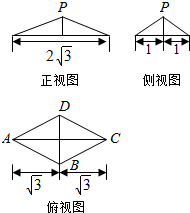 已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.
已知四棱锥P-ABCD的三视图如图所示,其中俯视图是菱形,正视图和侧视图都是等腰三角形,已知M为BC上一点,且BM=$\frac{1}{2}$,PA⊥PM.