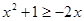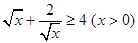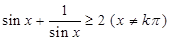题目内容
若不等式x2+2xy≤a(x2+y2)对于一切正数x,y恒成立,则实数a的最小值为________.

方法一:令y=tx,则t>0,代入不等式得x2+2tx2≤a(x2+t2x2),消掉x2得1+2t≤a(1+t2),即at2-2t+a-1≥0对t>0恒成立,显然a>0,故只要Δ=4-4a(a-1)≤0,即a2-a-1≥0,考虑到a>0,得a≥ .
.
方法二:令y=tx,则a≥ ,令m=1+2t>1,则t=
,令m=1+2t>1,则t= ,
,
则a≥ =
= ≤
≤ =
= ,
,
故a≥ .
.
 .
.方法二:令y=tx,则a≥
 ,令m=1+2t>1,则t=
,令m=1+2t>1,则t= ,
,则a≥
 =
= ≤
≤ =
= ,
,故a≥
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ 的最小值是 .
的最小值是 .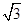 ,则
,则 的最大值为( )
的最大值为( )

 的最小值为________.
的最小值为________.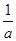 +
+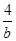 的最小值为________.
的最小值为________.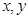 满足
满足 ,则
,则 的最小值为 .
的最小值为 . ≤λ恒成立,则λ的取值范围是________.
≤λ恒成立,则λ的取值范围是________. 有最大值
有最大值 ②函数
②函数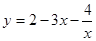 (
( )有最大值
)有最大值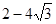 ③若
③若 ,则
,则 正确的序号是_____________.
正确的序号是_____________.