Question

【题目】定义在R上的奇函数f（x）满足f（x+1）=f（﹣x），当x∈（0，1）时，f（x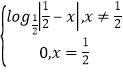）= ， 则f（x）在区间（1，）内是（　　）
A.增函数且f（x）＞0
B.增函数且f（x）＜0
C.减函数且f（x）＞0
D.减函数且f（x）＜0

Answer 1

【答案】D
【解析】解：由f（x）为奇函数，f（x+1）=f（﹣x）得，f（x）=﹣f（x+1）=f（x+2）；
∴f（x）=f（x+2）；
∴f（x）是周期为2的周期函数；
根据条件，x
∴
∴；
设2﹣x=t，t ， x=2﹣t；
∴；
∴；
∴
可以看出x增大时，-x减小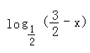，增大，f（x）减小；
∴在区间（1，）内，f（x）是减函数；
而由
∴；
∴f（x）＜0．
故选：D．
根据条件可以判断出f（x）是周期为2的周期函数，并且x从而可以得到f（x）=f（x﹣2）=﹣f（2﹣x）=可换元，令2﹣x=t，从而求出f（t）即得出x的解析式，从而可以判断此时的f（x）的单调性及其符号．