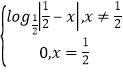题目内容
【题目】已知a+b=1,对a,b∈(0,+∞),![]() +
+![]() ≥|2x﹣1|﹣|x+1|恒成立,
≥|2x﹣1|﹣|x+1|恒成立,
(Ⅰ)求![]() +
+![]() 的最小值;
的最小值;
(Ⅱ)求x的取值范围.
【答案】解:(Ⅰ)∵a>0,b>0且a+b=1
∴![]() +
+![]() =(a+b)(
=(a+b)(![]() +
+![]() )=5+
)=5+![]()
当且仅当b=2a时等号成立,又a+b=1,即a=![]() ,b=
,b=![]() 时,等号成立,
时,等号成立,
故![]() +
+![]() 的最小值为9.
的最小值为9.
(Ⅱ)因为对a,b∈(0,+∞),使![]() +
+![]()
![]() 恒成立,
恒成立,
所以|2x﹣1|﹣|x+1|≤9,
当 x≤﹣1时,2﹣x≤9,∴﹣7≤x≤﹣1,
当 ![]() 时,﹣3x≤9,∴
时,﹣3x≤9,∴![]() ,
,
当 ![]() 时,x﹣2≤9,∴
时,x﹣2≤9,∴![]() ,∴﹣7≤x≤11.
,∴﹣7≤x≤11.
【解析】(Ⅰ)利用“1”的代换,化简![]() +
+![]() , 结合基本不等式求解表达式的最小值;
, 结合基本不等式求解表达式的最小值;
(Ⅱ)利用第一问的结果.通过绝对值不等式的解法,即可求x的取值范围。

练习册系列答案
相关题目