题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.(12分)
)中恰有三点在椭圆C上.(12分)
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l过定点.
【答案】
(1)
解:根据椭圆的对称性,P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )两点必在椭圆C上,
)两点必在椭圆C上,
又P4的横坐标为1,∴椭圆必不过P1(1,1),
∴P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )三点在椭圆C上.
)三点在椭圆C上.
把P2(0,1),P3(﹣1, ![]() )代入椭圆C,得:
)代入椭圆C,得:
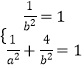 ,解得a2=4,b2=1,
,解得a2=4,b2=1,
∴椭圆C的方程为 ![]() =1.
=1.
(2)
证明:①当斜率不存在时,设l:x=m,A(m,yA),B(m,﹣yA),
∵直线P2A与直线P2B的斜率的和为﹣1,
∴ ![]() =
= ![]() =
= ![]() =﹣1,
=﹣1,
解得m=2,此时l过椭圆右顶点,不存在两个交点,故不满足.
②当斜率存在时,设l:y=kx+b,(b≠1),A(x1,y1),B(x2,y2),
联立 ![]() ,整理,得(1+4k2)x2+8kbx+4b2﹣4=0,
,整理,得(1+4k2)x2+8kbx+4b2﹣4=0,
![]() ,x1x2=
,x1x2= ![]() ,
,
则 ![]() =
= ![]() =
= ![]()
=  =
= ![]() =﹣1,又b≠1,
=﹣1,又b≠1,
∴b=﹣2k﹣1,此时△=﹣64k,存在k,使得△>0成立,
∴直线l的方程为y=kx﹣2k﹣1,
当x=2时,y=﹣1,
∴l过定点(2,﹣1).
【解析】(1.)根据椭圆的对称性,得到P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )三点在椭圆C上.把P2(0,1),P3(﹣1,
)三点在椭圆C上.把P2(0,1),P3(﹣1, ![]() )代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
)代入椭圆C,求出a2=4,b2=1,由此能求出椭圆C的方程.
(2.)当斜率不存在时,不满足;当斜率存在时,设l:y=kx+b,(b≠1),联立 ![]() ,得(1+4k2)x2+8kbx+4b2﹣4=0,由此利用根的判别式、韦达定理、直线方程,结合已知条件能证明直线l过定点(2,﹣1).
,得(1+4k2)x2+8kbx+4b2﹣4=0,由此利用根的判别式、韦达定理、直线方程,结合已知条件能证明直线l过定点(2,﹣1).
【考点精析】本题主要考查了斜截式方程和椭圆的标准方程的相关知识点,需要掌握直线的斜截式方程:已知直线![]() 的斜率为
的斜率为![]() ,且与
,且与![]() 轴的交点为
轴的交点为![]() 则:
则:![]() ;椭圆标准方程焦点在x轴:
;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

【题目】已知关于![]() 与
与![]() 有表格中的数据,且
有表格中的数据,且![]() 与
与![]() 线性相关,由最小二乘法得
线性相关,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 与
与![]() 的线性回归方程;
的线性回归方程;
(2)现有第二个线性模型:![]() ,且
,且![]() .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由