题目内容
(本小题满分12分)
已知常数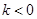 ,函数
,函数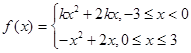
(1)求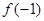 ,
,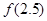 的值;
的值;
(2)讨论函数 在
在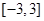 上的单调性;
上的单调性;
(3)求出 在
在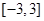 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
已知常数
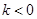 ,函数
,函数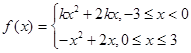
(1)求
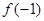 ,
,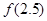 的值;
的值; (2)讨论函数
 在
在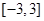 上的单调性;
上的单调性;(3)求出
 在
在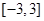 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.(1)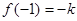 ,
,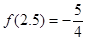
(2)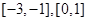 上为增函数,在
上为增函数,在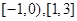 上为减函数
上为减函数
(3)①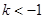 时,
时, 在
在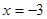 处取得最小值
处取得最小值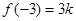 ,在
,在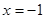 处取得最大值
处取得最大值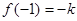
②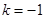 时,
时, 在
在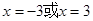 处取得最小值
处取得最小值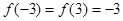 ,
,
在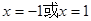 处取得最大值
处取得最大值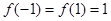
③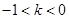 时,
时, 在
在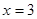 处取得最小值
处取得最小值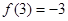 ,在
,在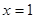 处取得最大值
处取得最大值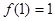 .
.
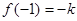 ,
,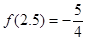
(2)
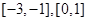 上为增函数,在
上为增函数,在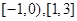 上为减函数
上为减函数 (3)①
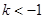 时,
时, 在
在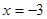 处取得最小值
处取得最小值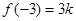 ,在
,在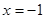 处取得最大值
处取得最大值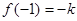
②
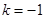 时,
时, 在
在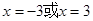 处取得最小值
处取得最小值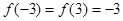 ,
,在
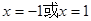 处取得最大值
处取得最大值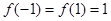
③
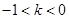 时,
时, 在
在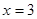 处取得最小值
处取得最小值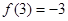 ,在
,在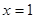 处取得最大值
处取得最大值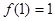 .
.试题分析:(1)
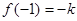 ,
,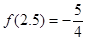
(2)∵
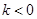 ,∴
,∴ 在
在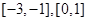 上为增函数,在
上为增函数,在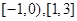 上为减函数
上为减函数(3)由函数
 在
在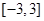 上的单调性可知,
上的单调性可知, 在
在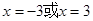 处取得最小值
处取得最小值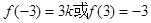 ,而在
,而在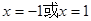 处取得最大值
处取得最大值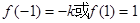
故有
①
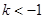 时,
时, 在
在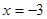 处取得最小值
处取得最小值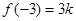 ,在
,在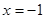 处取得最大值
处取得最大值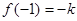
②
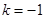 时,
时, 在
在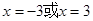 处取得最小值
处取得最小值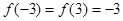 ,
,在
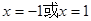 处取得最大值
处取得最大值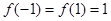
③
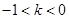 时,
时, 在
在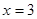 处取得最小值
处取得最小值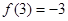 ,在
,在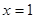 处取得最大值
处取得最大值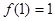 .
.点评:中档题,二次函数的最值问题,往往有“轴定区间动”、“轴动区间定”等不同情况,关键是讨论对称轴与给定区间的相对位置。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 的函数
的函数 对任意
对任意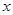 都有
都有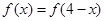 ,且其导函数
,且其导函数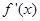 满足
满足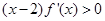 ,则当
,则当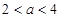 时,有( )
时,有( )
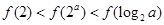
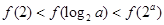
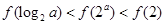
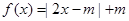 .
.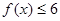 的解集为
的解集为 ,求实数
,求实数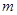 的值;
的值;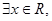 使
使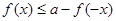 能成立,求实数a的取值范围.
能成立,求实数a的取值范围.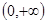 为增函数的是( )
为增函数的是( )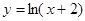

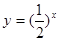
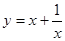
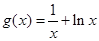 ,
,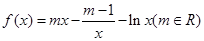 .
.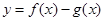 在
在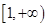 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;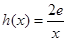 ,若在
,若在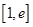 上至少存在一个
上至少存在一个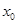 ,使得
,使得 成立,求
成立,求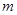 的取值范围.
的取值范围.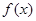 在
在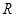 上是减函数,则满足
上是减函数,则满足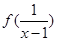 >
>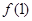 的实数
的实数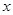 的取值范围是( ).
的取值范围是( ).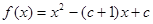
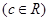 .
.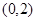 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;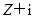 在映射f下的象为
在映射f下的象为 ,则
,则 的原象为
的原象为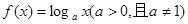 在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是
在(0,+∞)上单调递增,则f (a+1)与f (2)的大小关系是