题目内容
定义域为 的函数
的函数 对任意
对任意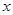 都有
都有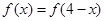 ,且其导函数
,且其导函数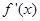 满足
满足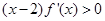 ,则当
,则当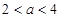 时,有( )
时,有( )
 的函数
的函数 对任意
对任意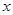 都有
都有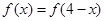 ,且其导函数
,且其导函数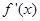 满足
满足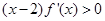 ,则当
,则当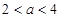 时,有( )
时,有( )A. | B.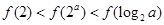 |
C.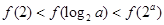 | D.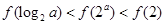 |
D
试题分析:因为定义域为
 的函数
的函数 对任意
对任意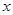 都有
都有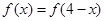 ,所以,函数图像关于x=2对称。又导函数
,所以,函数图像关于x=2对称。又导函数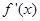 满足
满足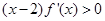 ,所以x>2时,
,所以x>2时,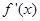 >0,函数为增函数;x<2时,
>0,函数为增函数;x<2时,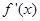 <0,函数为减函数。
<0,函数为减函数。当
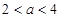 时,
时,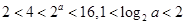 ,
,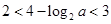 ,所以
,所以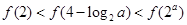 ,即
,即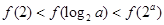 ,故选C。
,故选C。点评:典型题,本题综合考查了函数的图象和性质,导数应用于研究函数单调性,指数函数、对数函数的性质。考查覆盖面广,重点也突出,是一道难得的好题。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
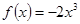 的图象
的图象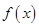 是定义在
是定义在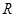 上的函数,且
上的函数,且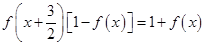 ,
,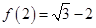 ,则
,则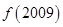 值为( )
值为( )
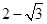
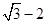
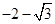
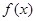 是定义在
是定义在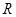 上的偶函数,当
上的偶函数,当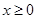 时,
时,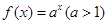 .
.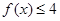 的解集为
的解集为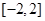 ,求
,求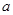 的值.
的值.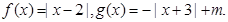
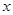 的不等式
的不等式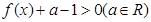 ;
;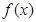 的图象恒在函数
的图象恒在函数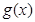 图象的上方(没有公共点),求
图象的上方(没有公共点),求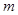 的取值范围。
的取值范围。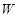 与它的航行速度
与它的航行速度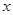 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;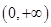 不是增函数的是( )
不是增函数的是( )
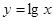
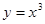
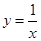
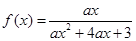 的定义域为
的定义域为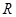 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
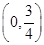
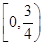
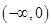
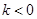 ,函数
,函数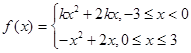
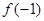 ,
,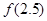 的值;
的值;  在
在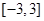 上的单调性;
上的单调性;