题目内容
下列命题正确的是（ ）
A、若向量
| ||||||||||||
B、若
| ||||||||||||
C、若果非零向量
| ||||||||||||
D、在△ABC中，必有
|
考点：命题的真假判断与应用
专题：平面向量及应用
分析：A，利用向量关系的概念可判断A；
B，若
=
，其方向任意，当
≠
时，满足前者，却不满足后者，可判断B；
C，令
=λ
（λ≠0，
≠
），则
+
=（1+λ）
，分λ＞-1、λ=-1、λ＜-1三类讨论后可判断C；
D，在△ABC中，必有
+
+
=
≠0，可判断D．
B，若
| b |
| 0 |
| a |
| 0 |
C，令
| a |
| b |
| b |
| 0 |
| a |
| b |
| b |
D，在△ABC中，必有
| AB |
| BC |
| CA |
| 0 |
解答：
解：A，若向量
与
是共线向量，则AB∥CD，或点A，B，C，D在同一条直线上，故A错误；
B，若
与
平行，则
，
的方向相同或相反，错误，原因是：若
=
，其方向任意，当
≠
时，
与
=
平行，但
的方向不是任意的；
C，若果非零向量
与
的方向相同或相反，即
=λ
（λ≠0，
≠
），
则
+
=（1+λ）
，
当λ＞-1时，
+
的方向与
的方向相同；
当λ＜-1时，
+
的方向与
的方向相同；
当λ=-1时，
+
=
，其方向任意，可与
，
之一的方向相同，
故
+
的方向必与
，
之一的方向相同，故C正确．
D，在△ABC中，必有
+
+
=
，故D错误；
故选：C．
| AB |
| CD |
B，若
| a |
| b |
| a |
| b |
| b |
| 0 |
| a |
| 0 |
| a |
| b |
| 0 |
| a |
C，若果非零向量
| a |
| b |
| a |
| b |
| b |
| 0 |
则
| a |
| b |
| b |
当λ＞-1时，
| a |
| b |
| b |
当λ＜-1时，
| a |
| b |
| a |
当λ=-1时，
| a |
| b |
| 0 |
| a |
| b |
故
| a |
| b |
| a |
| b |
D，在△ABC中，必有
| AB |
| BC |
| CA |
| 0 |
故选：C．
点评：本题考查命题的真假判断与应用，着重考查平面向量的共线的概念的理解与应用，特别是
，其方向任意，是易错点．
| 0 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
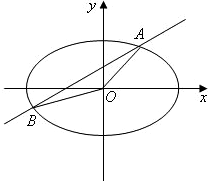如图，直线y=x+b与椭圆