题目内容

（2012•济南三模）如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：
①f（x）=sinxcosx；②f（x）=2sin（x+
π
4
）；③f（x）=sinx+
3
cosx；  ④f（x）=
2
sin2x+1．
其中“同簇函数”的是（　　）
分析：根据题意，能构成“同簇函数”的两个函数的图象形状和大小都相同，可得它们的周期和振幅必定相同．因此将各项中函数的周期与振幅求出并加以比较，即可得到本题的答案．
解答：解：∵构成“同簇函数”的两个函数图象经过平移后能够重合，
∴能构成“同簇函数”的两个函数的图象形状和大小都相同，可得它们的周期和振幅必定相同
因此，将各个函数化简整理，得
①f（x）=sinxcosx=
1
2
sin2x，周期为π，振幅是
1
2
；
②f（x）=2sin（x+
π
4
）的周期为2π，振幅为2；
③f（x）=sinx+
3
cosx=2（sinxcos
π
3
+cosxsin
π
3
）=2sin（x+
π
3
），周期为2π，振幅为2；
④f（x）=
2
sin2x+1的周期为π，振幅为
2
．
由此可得，②③的两个函数的周期和振幅都相同，它们是“同簇函数”
故选：C
点评：本题给出“同簇函数”的定义，要我们从几个函数中找出符合题意的函数，着重考查了三角函数的恒等变形，三角函数的图象与性质等知识，属于基础题．
练习册系列答案
相关题目
（2012•济南三模）经市场调查，某旅游城市在过去的一个月内（以30天计），第t天（1≤t≤30，t∈N﹢）的旅游人数f（t） （万人）近似地满足f（t）=4+
1t
，而人均消费g（t）（元）近似地满足g（t）=120-|t-20|．
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．
（2012•济南三模）某旅游景点预计2013年1月份起前x个月的旅游人数的和p（x）（单位：万人）与x的关系近似地满足p（x）=
1
2
x（x+1）•（39-2x），（x∈N*，且x≤12）．已知第x月的人均消费额q（x）（单位：元）与x的近似关系是q（x）=
35-2x(x∈N*，且1≤x≤6)
160
x
(x∈N*，且7≤x≤12)

（I）写出2013年第x月的旅游人数f（x）（单位：人）与x的函数关系式；
（II）试问2013年第几月旅游消费总额最大，最大月旅游消费总额为多少元？
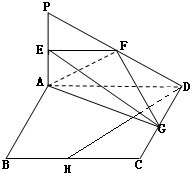（2012•济南三模）如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD，E、F、G、H分别是线段PA、PD、CD、BC的中点．
（Ⅰ）求证：BC∥平面EFG；
（Ⅱ）求证：DH⊥平面AEG；
（Ⅲ）求三棱锥E-AFG与四棱锥P-ABCD的体积比．
（2012•济南三模）已知直线l：y=x+1，圆O：x2+y2=
3
2
，直线l被圆截得的弦长与椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的短轴长相等，椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，-
1
3
）的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过定点T？若存在，求出点T的坐标；若不存在，请说明理由．
（2012•济南三模）设函数f（x）=x2-2（-1）klnx（k∈N*），f′（x）表示f（x）导函数．
（I）求函数f（x）的单调递增区间；
（Ⅱ）当k为偶数时，数列{an}满足a1=1，anf′(an)
=a
2
n+1
-3．证明：数列{
a
2
n
}中不存在成等差数列的三项；
（Ⅲ）当k为奇数时，设bn=
1
2
f′(n)-n，数列{bn}的前n项和为Sn，证明不等式(1+bn)
1
bn+1
＞e对一切正整数n均成立，并比较S2012-1与ln2012的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网