题目内容
（2012•济南三模）经市场调查，某旅游城市在过去的一个月内（以30天计），第t天（1≤t≤30，t∈N﹢）的旅游人数f（t） （万人）近似地满足f（t）=4+
，而人均消费g（t）（元）近似地满足g（t）=120-|t-20|．
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．
| 1 | t |
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．
分析：（1）根据该城市的旅游日收益=日旅游人数×人均消费的钱数得w（t）与t的解析式；
（2）因为w（t）中有一个绝对值，讨论t的取值，化简得W（t）为分段函数，第一段运用基本不等式求出最值，第二段是一个递减的函数求出最值比较即可．
（2）因为w（t）中有一个绝对值，讨论t的取值，化简得W（t）为分段函数，第一段运用基本不等式求出最值，第二段是一个递减的函数求出最值比较即可．
解答：解：（1）由题意，根据该城市的旅游日收益=日旅游人数×人均消费的钱数可得W（t）=f（t）g（t）=（4+
）（120-|t-20|）=
（2）当t∈[1，20]时，401+4t+
≥401+2
=441（t=5时取最小值）
当t∈（20，30]时，因为W（t）=559+
-4t递减，所以t=30时，W（t）有最小值W（30）=443
∵443
＞441
∴t∈[1，30]时，W（t）的最小值为441万元．
| 1 |
| t |
|
（2）当t∈[1，20]时，401+4t+
| 100 |
| t |
4t×
|
当t∈（20，30]时，因为W（t）=559+
| 140 |
| t |
| 2 |
| 3 |
∵443
| 2 |
| 3 |
∴t∈[1，30]时，W（t）的最小值为441万元．
点评：本题考查学生根据实际情况选择函数类型的能力，以及基本不等式在求函数最值中的应用能力，属于中档题．
练习册系列答案
相关题目
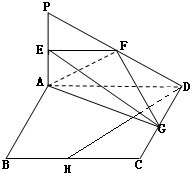（2012•济南三模）如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD，E、F、G、H分别是线段PA、PD、CD、BC的中点．