题目内容
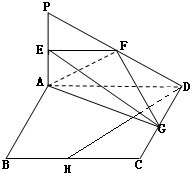 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.(Ⅰ)求证:BC∥平面EFG;
(Ⅱ)求证:DH⊥平面AEG;
(Ⅲ)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
分析:(Ⅰ)利用平行公理证明BC∥EF,再利用线面平行的判定,证明BC∥平面EFG;
(Ⅱ)利用PA⊥平面ABCD,证明AE⊥DH,利用△ADG≌△DCH,证明DH⊥AG,从而可证DH⊥平面AEG;
(Ⅲ)
=
,计算出体积可得结论.
(Ⅱ)利用PA⊥平面ABCD,证明AE⊥DH,利用△ADG≌△DCH,证明DH⊥AG,从而可证DH⊥平面AEG;
(Ⅲ)
| VE-APG |
| VP-ABCD |
| VG-AEF |
| VP-ABCD |
解答:(Ⅰ)证明:∵BC∥AD,AD∥EF,∴BC∥EF…(2分)
∵BC?平面EFG,EF?平面EFG,
∴BC∥平面EFG…(3分)
(Ⅱ)证明:∵PA⊥平面ABCD,DH?平面ABCD,
∴PA⊥DH,即 AE⊥DH…(5分)
∵△ADG≌△DCH,∴∠HDC=∠DAG,∠AGD+∠DAG=90°
∴∠AGD+∠HDC=90°
∴DH⊥AG
又∵AE∩AG=A,
∴DH⊥平面AEG…(8分)
(Ⅲ)解:
=
=
=
=
=
…(12分)
∵BC?平面EFG,EF?平面EFG,
∴BC∥平面EFG…(3分)
(Ⅱ)证明:∵PA⊥平面ABCD,DH?平面ABCD,
∴PA⊥DH,即 AE⊥DH…(5分)
∵△ADG≌△DCH,∴∠HDC=∠DAG,∠AGD+∠DAG=90°
∴∠AGD+∠HDC=90°
∴DH⊥AG
又∵AE∩AG=A,
∴DH⊥平面AEG…(8分)
(Ⅲ)解:
| VE-AFG |
| VP-ABCD |
| VG-AEF |
| VP-ABCD |
| ||
|
| ||||
| PA×AD×CD |
| ||||||||
| PA×AD×CD |
| 1 |
| 16 |
点评:本题考查线面平行,线面垂直,考查体积的计算,解题的关键是正确运用线面平行、线面垂直的判定,属于中档题.

练习册系列答案
相关题目