题目内容
(2012•济南三模)已知直线l:y=x+1,圆O:x2+y2=
,直线l被圆截得的弦长与椭圆C:
+
=1(a>b>0)的短轴长相等,椭圆的离心率e=
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点M(0,-
)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点M(0,-
| 1 |
| 3 |
分析:(Ⅰ)由题设可知b=1,利用e=
,即可求得椭圆C的方程;
(Ⅱ)先猜测T的坐标,再进行验证.若直线l的斜率存在,设其方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的坐标运算公式即可证得.
| ||
| 2 |
(Ⅱ)先猜测T的坐标,再进行验证.若直线l的斜率存在,设其方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的坐标运算公式即可证得.
解答:解:(Ⅰ)则由题设可知b=1,(2分)
又e=
,∴
=
,∴a2=4 (3分)
所以椭圆C的方程是
+y2=1.…(4分)
(Ⅱ)若直线l与y轴重合,则以AB为直径的圆是x2+y2=1①
若直线l垂直于y轴,则以AB为直径的圆是x2+(y+
)2=
②…(6分)
由①②解得
.
由此可知所求点T如果存在,只能是(0,1).…(7分)
事实上点T(0,1)就是所求的点.证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为x2+y2=1,过点T(0,1);
当直线l的斜率存在,设直线方程为y=kx-
,代入椭圆方程,并整理,得(18k2+9)x2-12kx-16=0(8分)
设点A、B的坐标分别为A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
∵
=(x1,y1-1),
=(x2,y2-1)
∴
•
=x1x2+(y1-1)(y2-1)=(k2+1)x1x2-
(x1+x2)+
=
=0
∴
⊥
,即以AB为直径的圆恒过定点T(0,1).…(11分)
综上可知,在坐标平面上存在一个定点T(0,1)满足条件.…(12分)
又e=
| ||
| 2 |
| a2-1 |
| a2 |
| 3 |
| 4 |
所以椭圆C的方程是
| x2 |
| 4 |
(Ⅱ)若直线l与y轴重合,则以AB为直径的圆是x2+y2=1①
若直线l垂直于y轴,则以AB为直径的圆是x2+(y+
| 1 |
| 3 |
| 16 |
| 9 |
由①②解得
|
由此可知所求点T如果存在,只能是(0,1).…(7分)
事实上点T(0,1)就是所求的点.证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为x2+y2=1,过点T(0,1);
当直线l的斜率存在,设直线方程为y=kx-
| 1 |
| 3 |
设点A、B的坐标分别为A(x1,y1),B(x2,y2),则x1+x2=
| 12k |
| 18k2+9 |
| -16 |
| 18k2+9 |
∵
| TA |
| TB |
∴
| TA |
| TB |
| 4 |
| 3 |
| 16 |
| 9 |
| -16k2-16-16k2+32k2+16 |
| 18k2+9 |
∴
| TA |
| TB |
综上可知,在坐标平面上存在一个定点T(0,1)满足条件.…(12分)
点评:本小题主要考查椭圆的标准方程、向量的坐标运算、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
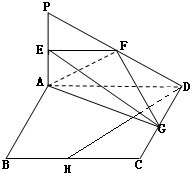 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.