题目内容
(2012•济南三模)设函数f(x)=x2-2(-1)klnx(k∈N*),f′(x)表示f(x)导函数.
(I)求函数f(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,anf′(an)
-3.证明:数列{
}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,设bn=
f′(n)-n,数列{bn}的前n项和为Sn,证明不等式(1+bn)
>e对一切正整数n均成立,并比较S2012-1与ln2012的大小.
(I)求函数f(x)的单调递增区间;
(Ⅱ)当k为偶数时,数列{an}满足a1=1,anf′(an)
| =a | 2 n+1 |
| a | 2 n |
(Ⅲ)当k为奇数时,设bn=
| 1 |
| 2 |
| 1 |
| bn+1 |
分析:(I)先求函数f(x)的导数,f′(x),再对k进行奇偶数讨论:1°当k 为奇数时;2°当k 为偶数时;分别得出导数值为正或负时的x的取值集合,最后综合即可;
(II)当k 为偶数时,由(1)知f′(x),由条件得{an 2+1}是一个公比为2的等比数列,从而得到an2=2n-1,最后利用反证法进行证明即可;
(Ⅲ) 当k为奇数时,f′(x)=2(x+
),要证(1+bn)
>e,即证(1+
)n+1>e,两边取对数,即证ln(1+
)>
,设1+
=t,构造函数g(t)=lnt+
-1,利用导数工具研究其单调性即可证得lnt>1-
,最后利用累乘法即可证出S2012-1<ln2012.
(II)当k 为偶数时,由(1)知f′(x),由条件得{an 2+1}是一个公比为2的等比数列,从而得到an2=2n-1,最后利用反证法进行证明即可;
(Ⅲ) 当k为奇数时,f′(x)=2(x+
| 1 |
| x |
| 1 |
| bn+1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| t |
| 1 |
| t |
解答:解:(I)函数f(x)的定义域为(0,+∞),又f′(x)=2x-2(-1)k
=
,
1°当k 为奇数时,f′(x)=
,∵x∈(0,+∞),∴f′(x)>0恒成立;
2°当k 为偶数时,f′(x)=
,∵x+1>0,∴f′(x)>0得x>1,即f(x)的单调增区间为(1,+∞),
综上所述,当k 为奇数时,f(x)的单调增区间为(0,+∞),当k 为偶数时,即f(x)的单调增区间为(1,+∞),
(Ⅱ)当k 为偶数时,由(1)知f′(x)=2x-
,∴f′(an)=2an-
,
由条件得:2(an2-1)=a n+1 2-3,故有:an+1 2+1=2(an 2+1),
∴{an 2+1}是一个公比为2的等比数列,∴an2=2n-1,
假设数列{an2}中的存在三项ar 2,s 2,at 2,能构成等差数列
不妨设r<s<t,则2as 2=a r 2+at 2,
即2(2s-1)=2r-1+2t-1,∴2 s-r+1=1+2 t-r,
又s-r+1>0,t-r>0,∴2 s-r+1为偶数,1+2 t-r为奇数,故假设不成立,
因此,数列{an2}中的任意三项不能构成等差数列;
(Ⅲ) 当k为奇数时,f′(x)=2(x+
),
∴bn=
f′(n)-n=
,Sn=1+
+
+…+
要证(1+bn)
>e,即证(1+
)n+1>e,两边取对数,
即证ln(1+
)>
(10分)
设1+
=t,则n=
,
lnt>1-
(t>1),构造函数g(t)=lnt+
-1,
∵x>1,∴g′(t)=
-
>0
∴g(t)在(1,+∞)上是增函数,g(t)>g(1)>0
即lnt>1-
,∴(1+bn)
>e,
S2012-1=(1+
+
+…+
)-1=
+
+…+
,
∵ln(1+
)>
,∴
+
+…+
<ln2+ln(1+
)+…+ln(1+
)=ln2+ln
+…+ln
=ln(2×
×…×
)=ln2012,
∴
+
+…+
<ln2012,
| 1 |
| x |
| 2[x2-(-1)k] |
| x |
1°当k 为奇数时,f′(x)=
| 2(x2+1) |
| x |
2°当k 为偶数时,f′(x)=
| 2(x2-1) |
| x |
综上所述,当k 为奇数时,f(x)的单调增区间为(0,+∞),当k 为偶数时,即f(x)的单调增区间为(1,+∞),
(Ⅱ)当k 为偶数时,由(1)知f′(x)=2x-
| 2 |
| x |
| 2 |
| an |
由条件得:2(an2-1)=a n+1 2-3,故有:an+1 2+1=2(an 2+1),
∴{an 2+1}是一个公比为2的等比数列,∴an2=2n-1,
假设数列{an2}中的存在三项ar 2,s 2,at 2,能构成等差数列
不妨设r<s<t,则2as 2=a r 2+at 2,
即2(2s-1)=2r-1+2t-1,∴2 s-r+1=1+2 t-r,
又s-r+1>0,t-r>0,∴2 s-r+1为偶数,1+2 t-r为奇数,故假设不成立,
因此,数列{an2}中的任意三项不能构成等差数列;
(Ⅲ) 当k为奇数时,f′(x)=2(x+
| 1 |
| x |
∴bn=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
要证(1+bn)
| 1 |
| bn+1 |
| 1 |
| n |
即证ln(1+
| 1 |
| n |
| 1 |
| n+1 |
设1+
| 1 |
| n |
| 1 |
| t-1 |
lnt>1-
| 1 |
| t |
| 1 |
| t |
∵x>1,∴g′(t)=
| 1 |
| t |
| 1 |
| t2 |
∴g(t)在(1,+∞)上是增函数,g(t)>g(1)>0
即lnt>1-
| 1 |
| t |
| 1 |
| bn+1 |
S2012-1=(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
∵ln(1+
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
| 1 |
| 2 |
| 1 |
| 2012 |
| 3 |
| 2 |
| 2012 |
| 2011 |
=ln(2×
| 3 |
| 2 |
| 2012 |
| 2011 |
∴
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
点评:本小题主要考查等差关系的确定、利用导数研究函数的单调性、证明不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
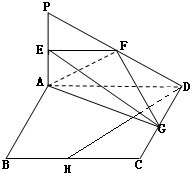 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.