题目内容
已知二次函数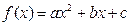 ,若对于任意的
,若对于任意的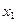 ,
,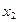
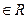 ,且
,且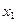
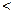
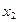 ,
,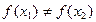 ,求证:存在
,求证:存在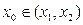 使得
使得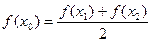
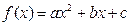 ,若对于任意的
,若对于任意的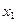 ,
,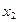
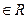 ,且
,且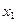
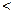
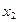 ,
,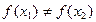 ,求证:存在
,求证:存在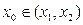 使得
使得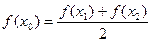
见解析
不妨设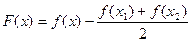
则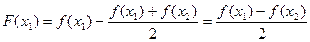
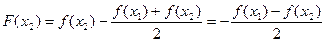
所以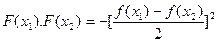 ,因为
,因为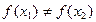
所以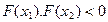 ,根据零点存在定理知存在
,根据零点存在定理知存在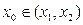 使得
使得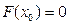
由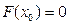 得
得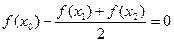 ,即
,即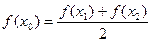
故存在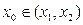 使得
使得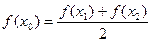
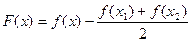
则
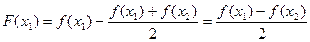
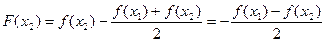
所以
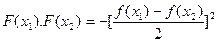 ,因为
,因为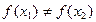
所以
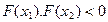 ,根据零点存在定理知存在
,根据零点存在定理知存在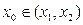 使得
使得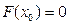
由
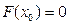 得
得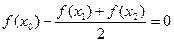 ,即
,即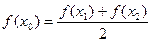
故存在
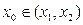 使得
使得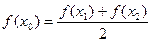

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
题目内容
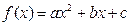 ,若对于任意的
,若对于任意的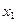 ,
,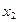
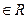 ,且
,且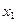
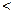
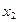 ,
,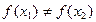 ,求证:存在
,求证:存在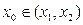 使得
使得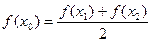
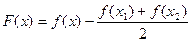
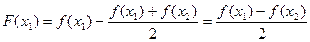
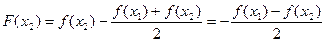
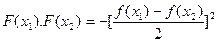 ,因为
,因为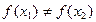
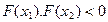 ,根据零点存在定理知存在
,根据零点存在定理知存在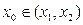 使得
使得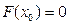
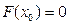 得
得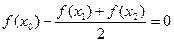 ,即
,即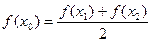
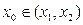 使得
使得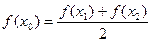

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案