题目内容
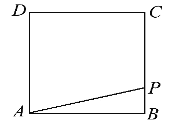
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?
【答案】（1）y=2x, y=8, y=24-2x. （2）x=3或x=9.
【解析】
（1）先求出定义域，根据点P的位置进行分类讨论，根据三角形的面积公式求出每一段△APB的面积与P移动的路程间的函数关系式，即可写出框图中①,②,③处应填充的式子.
（2）结合函数的解析式，建立等式，即可求出x的值.
解：（1）由题意,得函数的定义域为
，
当
时，
；
当
时，
；
当
时，
.
故程序框图中①,②,③处应填充的式子分别为:y=2x， y=8，y=24-2x.
(2)若输出的y值为6，则
当时，2x=6，解得x=3；
当时，24-2x=6, 解得x=9.
综上，输出的面积y值为6，则路程x的值为3或9.
练习册系列答案
相关题目
【题目】在某次测验中，有6位同学的平均成绩为75分．用xn表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学同学的成绩如表：
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
（1）求第6位同学的成绩x6及这6位同学成绩的标准差s；
（2）若从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间[68，75）中的概率．
