题目内容
【题目】已知数列{an}满足 an+2﹣an+1=an+1﹣an , n∈N* , 且a5= ![]() 若函数f(x)=sin2x+2cos2
若函数f(x)=sin2x+2cos2 ![]() ,记yn=f(an),则数列{yn}的前9项和为( )
,记yn=f(an),则数列{yn}的前9项和为( )
A.O
B.﹣9
C.9
D.1
【答案】C
【解析】解:∵数列{an}满足an+2﹣an+1=an+1﹣an , n∈N* , ∴数列{an}是等差数列,
∵a5= ![]() ,∴a1+a9=a2+a8=a3+a7=a4+a6=2a5=π
,∴a1+a9=a2+a8=a3+a7=a4+a6=2a5=π
∵f(x)=sin2x+2cos2 ![]() ,
,
∴f(x)=sin2x+cosx+1,
∴f(a1)+f(a9)=sin2a1+cosa1+1+sin2a9+cosa9+1=2
同理f(a2)+f(a8)=f(a3)+f(a7)=f(a4)+f(a6)=2
∵f(a5)=1
∴数列{yn}的前9项和为9
故选C.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系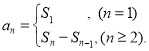 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】下面给出了2010年亚洲某些国家的国民平均寿命![]() 单位:岁
单位:岁![]() .
.
国家 | 平均寿命 | 国家 | 平均寿命 | 国家 | 平均寿命 |
阿曼 |
| 阿富汗 | 59 | 巴基斯坦 |
|
巴林 | | 阿联酋 |
| 马来西亚 |
|
朝鲜 |
| 东帝汶 |
| 孟加拉国 |
|
韩国 |
| 柬埔寨 |
| 塞浦路斯 |
|
老挝 |
| 卡塔尔 |
| 沙特阿拉伯 |
|
蒙古 |
| 科威特 | | 哈萨克斯坦 |
|
缅甸 |
| 菲律宾 |
| 印度尼西亚 |
|
日本 |
| 黎巴嫩 |
| 土库曼斯坦 | 65 |
泰国 |
| 尼泊尔 | 68 | 吉尔吉斯斯坦 |
|
约旦 |
| 土耳其 |
| 乌兹别克斯坦 |
|
越南 | 75 | 伊拉克 |
| 也门 |
|
中国 |
| 以色列 |
| 文莱 |
|
伊朗 | 74 | 新加坡 |
| 叙利亚 |
|
印度 |
|
![]() 根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:
根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 请根据上述所提供的数据,求出频率分布直方图中的a,b;
请根据上述所提供的数据,求出频率分布直方图中的a,b;
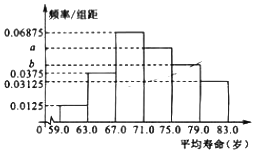
![]() 请根据统计思想,利用
请根据统计思想,利用![]() 中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数
中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数![]() 保留一位小数
保留一位小数![]() .
.



