题目内容
(12分)已知函数
的部分图象如下图所示。
(Ⅰ)求函数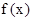 的解析式;
的解析式;
(Ⅱ)求函数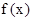 的单调递增区间;
的单调递增区间;
(Ⅲ)若不等式 在
在 上
上
恒成立,求实数m的取值范围。


的部分图象如下图所示。
(Ⅰ)求函数
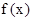 的解析式;
的解析式;(Ⅱ)求函数
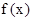 的单调递增区间;
的单调递增区间;(Ⅲ)若不等式
 在
在 上
上恒成立,求实数m的取值范围。

解:(Ⅰ)由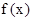 的图象可知
的图象可知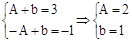 ∴f(x)=2sin(
∴f(x)=2sin(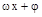 )+1 (1分)
)+1 (1分)
由“五点法”可知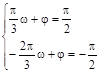 (3分)解得:
(3分)解得: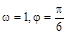 (4分)
(4分)
则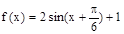 (5分)
(5分)
(Ⅱ)由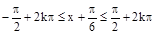 ,K∈Z,得
,K∈Z,得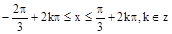 。
。
所以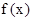 的单调递增区间为
的单调递增区间为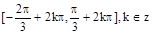 (8分)
(8分)
(Ⅲ)因为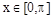 ,则
,则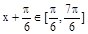 ,则
,则 故
故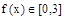 (10分)
(10分)
而不等式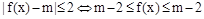 恒成立。
恒成立。
则需满足: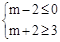 ,即
,即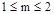 所以实数m的取值范围为[1,2] (12分
所以实数m的取值范围为[1,2] (12分
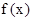 的图象可知
的图象可知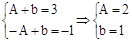 ∴f(x)=2sin(
∴f(x)=2sin(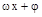 )+1 (1分)
)+1 (1分)由“五点法”可知
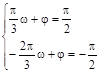 (3分)解得:
(3分)解得: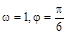 (4分)
(4分)则
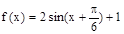 (5分)
(5分)(Ⅱ)由
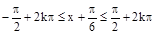 ,K∈Z,得
,K∈Z,得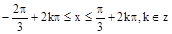 。
。所以
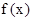 的单调递增区间为
的单调递增区间为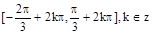 (8分)
(8分)(Ⅲ)因为
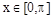 ,则
,则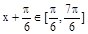 ,则
,则 故
故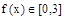 (10分)
(10分)而不等式
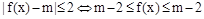 恒成立。
恒成立。则需满足:
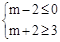 ,即
,即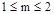 所以实数m的取值范围为[1,2] (12分
所以实数m的取值范围为[1,2] (12分略

练习册系列答案
相关题目
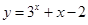 的零点所在的大致区间是(参考数据
的零点所在的大致区间是(参考数据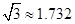 ,
,
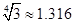 )
)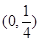
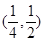
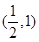
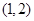
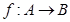 其中
其中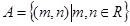 ,
,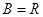 ,已知对所有的有序正整数对
,已知对所有的有序正整数对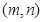 满足下述条件:
满足下述条件: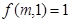 ; 2若
; 2若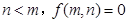
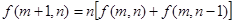
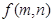 的表达式为 (用含n的代数式表示)
的表达式为 (用含n的代数式表示)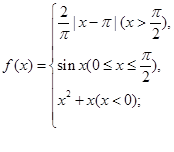
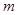 是非零常数,关于
是非零常数,关于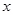 的方程
的方程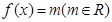 有且仅有三个不同的实数根,若
有且仅有三个不同的实数根,若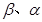 分别是三个根中的最小根和最大根,
分别是三个根中的最小根和最大根, 则
则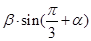 = .
= .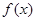 在区间
在区间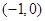 和
和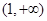 上递增,在区间
上递增,在区间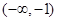 和
和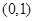 上递减,则
上递减,则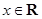 ,函数
,函数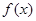 满足
满足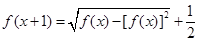 ,设
,设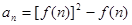 ,数列
,数列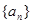 的前15项的和为
的前15项的和为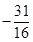 ,则
,则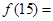 .
.