题目内容
函数 ;
;
(1)若 在
在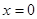 处取极值,求
处取极值,求 的值;
的值;
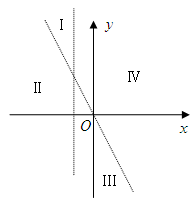
(2)设直线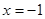 和
和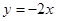 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若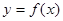 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的 的范围.
的范围.
(1)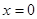 为极值点;(2)
为极值点;(2)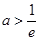 。
。
解析试题分析:(1)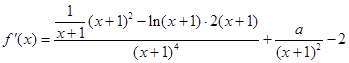
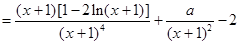
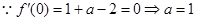
经检验,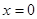 为极值点
为极值点
(2)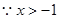 ,
, Ⅲ或Ⅳ,
Ⅲ或Ⅳ,
若图像在区域Ⅲ,则有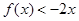 恒成立,
恒成立,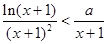 ,
, 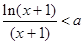 ,
,
设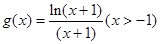 ,只要
,只要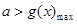 ,
,
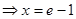 ,
,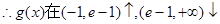 ,
,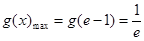 ,故
,故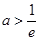
若图像在区域Ⅳ,则有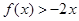 恒成立,
恒成立,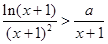 ,
, 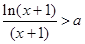 ,
,
设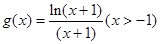 ,只要
,只要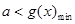 ,
, 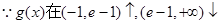 ,当
,当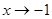 时,
时,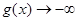 ,不会成立
,不会成立
综上所述 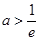
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。涉及不等式恒成立问题,利用“分离参数法”又转化成函数的最值问题。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目
 在
在 处取得极值.
处取得极值. 的值;
的值;  的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围; ,不等式
,不等式 都成立.
都成立.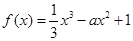
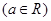 .
.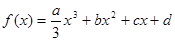 (
( >0),且方程
>0),且方程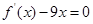 的两个根分别为1,4。
的两个根分别为1,4。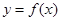 过原点时,求
过原点时,求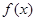 的解析式;
的解析式;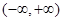 无极值点,求a的取值范围。
无极值点,求a的取值范围。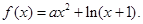
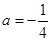 时,求函数
时,求函数 的单调区间;
的单调区间;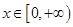 ,
,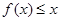 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 为偶函数,曲线
为偶函数,曲线 过点(2,5),
过点(2,5),  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数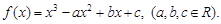 .
.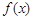 在
在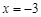 和
和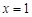 处取得极值,试求
处取得极值,试求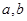 的值;
的值;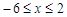 时,
时,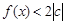 恒成立,求c的取值范围.
恒成立,求c的取值范围.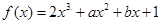 的导数为
的导数为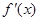 ,若函数
,若函数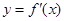 的图像关于直
的图像关于直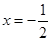 对称,且
对称,且 . (1)求实数
. (1)求实数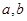 的值 ;(2)求函数
的值 ;(2)求函数 的极值.
的极值.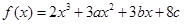 在
在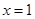 及
及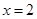 时取得极值.
时取得极值.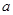 、b的值;
、b的值;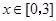 ,都有
,都有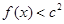 成立,求c的取值范围.
成立,求c的取值范围.