题目内容
设定函数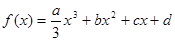 (
( >0),且方程
>0),且方程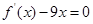 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当 =3且曲线
=3且曲线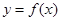 过原点时,求
过原点时,求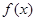 的解析式;
的解析式;
(Ⅱ)若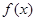 在
在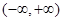 无极值点,求a的取值范围。
无极值点,求a的取值范围。
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:由 得
得 
因为 的两个根分别为1,4,所以
的两个根分别为1,4,所以 (*)
(*)
(Ⅰ)当 时,又由(*)式得
时,又由(*)式得
解得
又因为曲线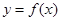 过原点,所以
过原点,所以
故
(Ⅱ)由于a>0,所以“ 在(-∞,+∞)内无极值点”等价于“
在(-∞,+∞)内无极值点”等价于“ 在(-∞,+∞)内恒成立”。
在(-∞,+∞)内恒成立”。
由(*)式得 。
。
又
解 得
得
即 的取值范围
的取值范围
考点:本题主要考查应用导数研究函数的单调性及极值,待定系数法。
点评:典型题,本题属于导数应用中的基本问题,(II)将函数问题转化成不等式恒成立问题,通过对方程实根的讨论及研究,确定得到参数的范围。

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.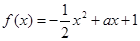 ,
,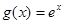 ,
,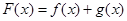 .
.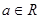
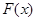 在
在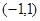 存在极值,求
存在极值,求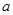 的取值范围;
的取值范围; 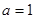 ,问是否存在与曲线
,问是否存在与曲线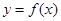 和
和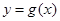 都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。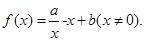 ,其中
,其中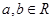
 在点
在点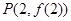 处的切线方程为
处的切线方程为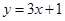 ,求函数
,求函数 的解析式;
的解析式;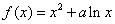
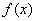 +
+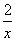 在
在 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.  .
. 处的切线方程;
处的切线方程; ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点 ,使得
,使得 成立,求实数p的取值范围.
成立,求实数p的取值范围. ;
;
 在
在 处取极值,求
处取极值,求 的值;
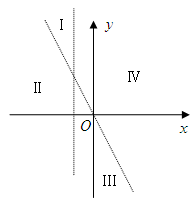
的值; 和
和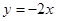 将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若
将平面分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域(不包括边界),若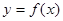 图象恰好位于其中一个区域,试判断其所在区域并求出相应的
图象恰好位于其中一个区域,试判断其所在区域并求出相应的 ,其中
,其中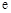 为自然对数的底数.
为自然对数的底数.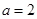 时,求曲线
时,求曲线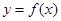 在
在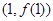 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;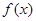 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为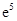 ,求
,求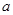 的
的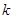 和
和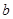 ,使得函数
,使得函数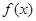 和
和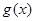 对其定义域上的任意实数
对其定义域上的任意实数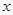 分别满足:
分别满足: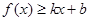 和
和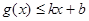 ,则称直线
,则称直线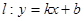 为
为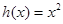 ,
,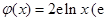 为自然对数的底数).
为自然对数的底数).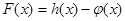 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.