Question

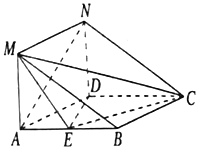
【题目】如图，已知圆锥的顶点为S，底面圆O的两条直径分别为AB和CD，且AB⊥CD，若平面平面．现有以下四个结论：

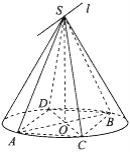
①AD∥平面SBC；

②；

③若E是底面圆周上的动点，则△SAE的最大面积等于△SAB的面积；

④与平面SCD所成的角为45°．

其中正确结论的序号是__________．

Answer 1

【答案】①②④

【解析】

利用线面平行判定定理说明①的正误；利用线面平行性质定理说明②的正误；由，讨论∠ASB的锐钝可说明③的正误；利用与平面SCD所成的角等于AD与平面SCD所成的角可判断④的正误.

由AB和CD是圆O得直径及AB⊥CD，得四边形ABCD为正方形，则AD∥BC，

从而AD∥平面SBC，则①正确；又因为平面SAD，且平面，所以，则②正确；因为，当∠ASB为钝角时，；

当∠ASB为锐角或直角时，，则③不正确；由，得与平面SCD所成的角等于AD与平面SCD所成的角，即为∠ADO，又因为∠ADO=45°，故④正确.

故答案为：①②④