题目内容
(选做题)如图,⊙O和⊙O'相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E。

证明:(1)AC·BD=AD·AB;
(2)AC=AE。
(2)AC=AE。
证明:(1)∵AC与⊙O'相切于点A,故∠CAB=∠ADB,
同理可得∠ACB=∠DAB,
∴△ACB∽△DAB,
∴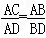 ,
,
∴AC?BD=AD?AB。
(2)∵AD与⊙O相切于点A,
∴∠AED=∠BAD,
又∠ADE=∠BDA,
∴△EAD∽△ABD,
∴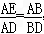 ,
,
∴AE?BD=AD?AB
再由(1)的结论AC?BD=AD?AB 可得,AC=AE。
同理可得∠ACB=∠DAB,
∴△ACB∽△DAB,
∴
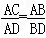 ,
, ∴AC?BD=AD?AB。
(2)∵AD与⊙O相切于点A,
∴∠AED=∠BAD,
又∠ADE=∠BDA,
∴△EAD∽△ABD,
∴
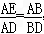 ,
,∴AE?BD=AD?AB
再由(1)的结论AC?BD=AD?AB 可得,AC=AE。

练习册系列答案
相关题目
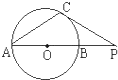 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)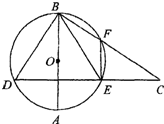 (2007•湛江二模)(几何证明选讲选做题)如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连接BC与圆0交于F,若∠CFE=α(
(2007•湛江二模)(几何证明选讲选做题)如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连接BC与圆0交于F,若∠CFE=α( (几何证明选做题)
(几何证明选做题)  (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)