题目内容
（几何证明选做题） 如图，⊙O的直径AB=6cm，P是延长线上的一点，过点P作⊙O的切线，切点为C，连结AC，若∠CAP=30°，则PC=
3
| 3 |
3
．| 3 |
分析：根据圆的切线的性质得到∠OCP=90°，由AO=CO且∠A=30°，算出∠ACO=30°，从而得出∠ACP=120°．利用△ACP的内角和算出∠P=30°，得到AC=CP．最后在△AOC中，利用正弦定理解出AC=3
，即可得到PC之长．
| 3 |
解答：解：∵PC是⊙O的切线，切点为C，∴OC⊥PC，得∠OCP=90°
∵△AOC中，AO=CO=3cm，∠A=30°
∴∠ACO=30°，∠AOC=120°
得∠ACP=120°，∠P=180°-（∠ACP+∠A）=30°
由此可得∠A=∠P=30°，得AC=CP
△AOC中，
=
，即
=
，得AC=3
∴CP=AC=3
，即PC=3
故答案为：3
∵△AOC中，AO=CO=3cm，∠A=30°
∴∠ACO=30°，∠AOC=120°
得∠ACP=120°，∠P=180°-（∠ACP+∠A）=30°
由此可得∠A=∠P=30°，得AC=CP
△AOC中，
| AC |
| sin∠AOC |
| CO |
| sinA |
| AC |
| sin120° |
| 3 |
| sin30° |
| 3 |
∴CP=AC=3
| 3 |
| 3 |
故答案为：3
| 3 |
点评：本题给出圆的切线满足的条件，求线段PC长．着重考查了圆的切线的性质、等腰三角形的性质与判定、三角形内角和定理与正弦定理解三角形等知识，属于中档题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
A．（不等式选做题）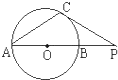
（2013•惠州一模）（几何证明选做题）
（考生注意：请在二题中任选一题作答，如果多做，则按所做的第一题评分）
（2012•宝鸡模拟）（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）