Question

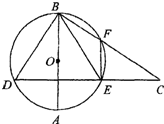（2007•湛江二模）（几何证明选讲选做题）如图，⊙O中，直径AB和弦DE互相垂直，C是DE延长线上一点，连接BC与圆0交于F，若∠CFE=α（α∈(0，

π

2

)），则∠DEB

α

．

Answer 1

分析：由题意可得，AB垂直平分DE，从而可得D=∠BED，由DEFB四点共圆可得∠EFC=∠D=α，可求

解答：解：∵直径AB和弦DE互相垂直
∴AB平分DE
∴BD=BE，∠D=∠BED
∵DEFB四点共圆
∴∠EFC=∠D=α
∴∠DEB=α
故答案为：α

点评：本题主要考查了垂径定理及四点共圆性质定理的应用，属于基础试题