题目内容
6．四面体ABCD中，AD=x，其余各棱长均为2，给出下列论断①x的取值范围是（0，$2\sqrt{3}$）；
②异面直线AB与CD成角最大为90°；
③直线AB与平面BCD成角最大为60°；
④体积最大时，二面角A-CD-B平面角的正切值为2．
其中正确的命题有①②③④（写出所有正确命题的序号）
分析 由题意画出图形，然后根据AB的变化情况进行分析，要构成四面体，A不能落在面BCD上，从而得到x的取值范围判断①的正误；判断泡沫之夏的位置关系，得到异面直线所成角，判断②的正误；利用直线与平面市场价 的，判断③的正误；找出体积最大时，二面角求解判断④的正误．
解答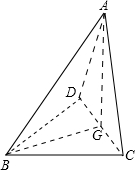 
解：对于①，如图，
四面体ABCD中，AD=AC=DC=BD=BC=2，
取CD中点G，连结AG，BG，
在等边三角形ACD和等边三角形BCD中，可求得AG=BG=$\sqrt{3}$，
∴要构成四面体ABCD，A，B不能重合，即x＞0，点A不能在平面BCD上，即AB＜AG+BG，x＜2$\sqrt{3}$．
∴①正确；
对于②，因为异面直线所成角的最大值是90°，当x=2时几何体是正四面体，异面直线AB⊥CD，异面直线AB与CD成角最大为90°．∴②正确．
对于③，当侧面ABC与底面BCD垂直时，AB与底面BDC所成角取得最大值，三角形ABC是正三角形，所以最大值为60°，∴③正确．
对于④，当侧面ABC与底面BCD垂直时，A到底面BCD的距离最大，底面BCD面积是定值，此时体积最大，
如图，作AO⊥BC于O，作OE⊥BD于E，连结AE，则二面角A-CD-B平面角为∠AEO，此时O是BC的中点，AO=2OE，二面角A-CD-B平面角的正切值为2，∴④正确；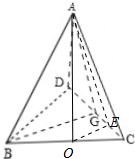
故答案为：①②③④．
点评 本题考查二面角，直线与平面所成角，异面直线所成角，点线面距离的求法，命题的真假判断与应用，考查了数形结合的解题思想方法，解答的关键在于动中求静，是中档题．
练习册系列答案
相关题目
如图，在棱长为a的正方体A1B1C1D1-ABCD中，
如图，在平面直角坐标系xOy中，F1，F2分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点，顶点B的坐标为（0，b），且△BF1F2是边长为2的等边三角形．
已知两点F1（-1，0）及F2（1，0），点P在以F1，F2为焦点的椭圆C上，且|PF1|+|PF2|=4．
如图，已知四边形AA1C1C和AA1B1B都是菱形，平面AA1B1B和平面AA1C1C互相垂直，且∠ACC1=∠BAA1=60°，AA1=2