题目内容
15. 如图,已知四边形AA1C1C和AA1B1B都是菱形,平面AA1B1B和平面AA1C1C互相垂直,且∠ACC1=∠BAA1=60°,AA1=2
如图,已知四边形AA1C1C和AA1B1B都是菱形,平面AA1B1B和平面AA1C1C互相垂直,且∠ACC1=∠BAA1=60°,AA1=2(Ⅰ)求证:AA1⊥BC1;
(Ⅱ)求四面体A-CC1B1的体积;
(Ⅲ)求二面角C-AB-C1的正弦值.
分析 (1)取AA1的中点为O,连接OB,通过已知条件及线面垂直的判定定理即得结论;
(2)利用三角形CC1B1和CC1B面积相等,通过体积公式计算即可;
(3)以O为坐标原点,分别以OA1,OC1,OB为x轴,y轴,z轴建立坐标系,利用平方关系,通过计算平面ABC的法向量与平面ABC1的法向量的夹角的余弦值即可.
解答 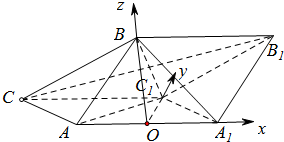 (1)证明:设AA1的中点为O,连接OB,
(1)证明:设AA1的中点为O,连接OB,
∵四边形AA1C1C和AA1B1B都是菱形,且∠ACC1=∠BAA1=60°,
∴三角形AA1B和三角形AA1C1都是等边三角形,
所以OB⊥OC1,
又∵OB∩OC1=O,∴AA1⊥平面OBC1,
所以AA1⊥BC1;
(2)解:∵三角形CC1B1和CC1B面积相等,
∴${V_{A-C{C_1}{B_1}}}$=${V_{A-C{C_1}{B_{\;}}}}={V_{B-C{C_1}{A_{\;}}}}=\frac{1}{3}{S_{AC{C_1}}}OB=1$,
∴四面体A-CC1B1的体积为1;
(3)解:由(1)知AA1⊥OB,
又∵平面AA1B1B和平面AA1C1C互相垂直,
∴OB⊥平面AA1C1C,
∴OA1,OC1,OB,三条直线两两垂直,
以O为坐标原点,分别以OA1,OC1,OB为x轴,y轴,z轴建立坐标系如图,
则$A(-1,0,0),B(0,0,\sqrt{3}),C(-2,\sqrt{3},0)$,${C_1}(0,\sqrt{3},0)$,
∴$\overrightarrow{AB}$=(1,0,$\sqrt{3}$),$\overrightarrow{AC}$=(-1,$\sqrt{3}$,0),$\overrightarrow{A{C}_{1}}$=(1,$\sqrt{3}$,0),
设平面ABC,ABC1的法向量$\overrightarrow m,\overrightarrow n$的坐标分别为(a,b,c),(a1,b1,c1),
由$\overrightarrow m⊥\overrightarrow{AB},\overrightarrow m⊥\overrightarrow{AC}$,可得$a+\sqrt{3}c=0,-a+\sqrt{3}b=0$,
所以可取$\overrightarrow m=(\sqrt{3},1,-1)$,
同理可取$\overrightarrow n=(\sqrt{3},-1,-1)$,
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{3}{5}$,
所以二面角C-AB-C1的正弦值为$\sqrt{1-(\frac{3}{5})^{2}}$=$\frac{4}{5}$.
点评 本题考查直线与平面垂直的判定,二面角的计算,考查四面体的体积公式,考查空间想象能力,计算能力,注意解题方法的积累,属于中档题.

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 如图,在三棱柱ABC-A1B1C1中,已知 AB=BC=1,CC1=2,AC1与平面 BCC1B1所成角为30°,AB⊥平面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知 AB=BC=1,CC1=2,AC1与平面 BCC1B1所成角为30°,AB⊥平面BB1C1C. 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是菱形,且∠BCD=120°,PA=AB,F、G分别是线段PD和BC上的动点且$\frac{PF}{PD}$=$\frac{BG}{BC}$=λ,λ∈(0,1).
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是菱形,且∠BCD=120°,PA=AB,F、G分别是线段PD和BC上的动点且$\frac{PF}{PD}$=$\frac{BG}{BC}$=λ,λ∈(0,1). 在多面体ABCDE中,CD⊥平面ABC,BE∥CD,AB=2$\sqrt{5}$,AC=4,BC=2,CD=4,BE=1.
在多面体ABCDE中,CD⊥平面ABC,BE∥CD,AB=2$\sqrt{5}$,AC=4,BC=2,CD=4,BE=1.