题目内容
16.在等腰梯形ABCD中,AD∥BC,AB=AD=$\frac{1}{2}$BC=2,E是BC的中点,将△BAE沿着AE翻折成△B1AE,是平面B1AE⊥平面AECD,M为线段AE的中点.(1)求证:CD⊥B1D;
(2)求二面角D-AB1-E的余弦值;
(3)在线段B1C上是否存在点P,使得直线MP∥平面B1AD?若存在,求出$\frac{{B}_{1}P}{{B}_{1}C}$的值,若不存在,请说明理由.

分析 (Ⅰ)证明CD⊥DM.B1M⊥CD.通过直线与平面垂直的判定定理证明CD⊥平面B1MD.
(Ⅱ)以ME为x轴,MD为y轴,MB1为z轴建立空间直角坐标系,求出平面AB1E的法向量,平面DB1A的法向量通过向量的数量积求解二面角D-AB1-E的余弦值.
(Ⅲ) 存在点P,使得MP∥平面B1AD,设在线段B1C上存在点P,使得MP∥平面B1AD,设$\overrightarrow{{B}_{1}P}$=λ$\overrightarrow{{B}_{1}C}$,(0≤λ≤1),通过$\overrightarrow{MP}•\overrightarrow{m}=0$,求出$\frac{{B}_{1}P}{{B}_{1}C}$=$\frac{1}{2}$即可.
解答 (Ⅰ)证明:由题意可知四边形ABED是平行四边形,所以AM=ME,故B1M⊥AE.
又因为AB=BE,M为AE的中点,所以BM⊥AE,
即DM⊥AE.又因为AD∥BC,AD=CE=2.
所以四边形ADCE是平行四边形.
所以AE∥CD.
故CD⊥DM.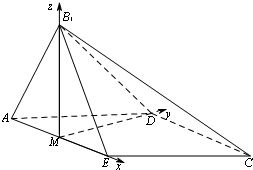
因为平面B1AE⊥平面AECD,平面B1AE∩平面AECD=AE,B1M?平面AECD
所以B1M⊥平面AECD.B1M⊥AE.
因为CD?平面AECD,所以B1M⊥CD.
因为MD∩B1M=M,MD、B1M?平面B1MD,
所以CD⊥平面B1MD.…(5分)
(Ⅱ)解:以ME为x轴,MD为y轴,MB1为z轴建立空间直角坐标系,则C(2,$\sqrt{3}$,0),B1(0,0,$\sqrt{3}$),A(-1,0,0),D(0,$\sqrt{3}$,0).
平面AB1E的法向量为$\overrightarrow{MD}$=(0,$\sqrt{3}$,0).
设平面DB1A的法向量为$\overrightarrow{m}$=(x,y,z),
因为$\overrightarrow{A{B}_{1}}$=(1,0,$\sqrt{3}$),$\overrightarrow{AD}$=(1,$\sqrt{3}$,0),
所以$\left\{\begin{array}{l}{x+\sqrt{3}z=0}\\{x+\sqrt{3}y=0}\end{array}\right.$,
令z=1得,$\overrightarrow{m}$=(-$\sqrt{3}$,1,1).
所以cos<$\overrightarrow{m}$,$\overrightarrow{MD}$>=$\frac{\sqrt{5}}{5}$,因为二面角D-AB1-E为锐角,
所以二面角D-AB1-E的余弦值为$\frac{\sqrt{5}}{5}$.…(10分)
(Ⅲ)解:存在点P,使得MP∥平面B1AD.…(11分)
设在线段B1C上存在点P,使得MP∥平面B1AD,
设$\overrightarrow{{B}_{1}P}$=λ$\overrightarrow{{B}_{1}C}$,(0≤λ≤1),C(2,$\sqrt{3}$,0),
因为$\overrightarrow{MP}$=$\overrightarrow{M{B}_{1}}$+$\overrightarrow{{B}_{1}P}$.
所以$\overrightarrow{MP}$=(2λ,$\sqrt{3}$λ,$\sqrt{3}$-$\sqrt{3}$λ),
因为MP∥平面B1AD,所以$\overrightarrow{MP}•\overrightarrow{m}=0$,
所以-2$\sqrt{3}$λ+$\sqrt{3}$λ+$\sqrt{3}$-$\sqrt{3}$λ=0,解得λ=$\frac{1}{2}$,
又因为MP?平面B1AD,
所以在线段B1C上存在点P,使得MP∥平面B1AD,$\frac{{B}_{1}P}{{B}_{1}C}$=$\frac{1}{2}$.…(14分)
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,存在性问题的判断与证明,考查空间想象能力.

| A. | 4×20152-1 | B. | 4×20142-1 | C. | 4×20132-1 | D. | 4×20132 |
 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是菱形,且∠BCD=120°,PA=AB,F、G分别是线段PD和BC上的动点且$\frac{PF}{PD}$=$\frac{BG}{BC}$=λ,λ∈(0,1).
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是菱形,且∠BCD=120°,PA=AB,F、G分别是线段PD和BC上的动点且$\frac{PF}{PD}$=$\frac{BG}{BC}$=λ,λ∈(0,1). 如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,BC=2,又AC=CD=DE=1,ACB=120°,CD⊥AB.
如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,BC=2,又AC=CD=DE=1,ACB=120°,CD⊥AB. 为了解某市公益志愿者的年龄分布情况,从全市志愿者中随机抽取了80名志愿者,对其年龄进行统计后得到频率分布直方图如下,但是年龄组在[25,30)的数据不慎丢失.
为了解某市公益志愿者的年龄分布情况,从全市志愿者中随机抽取了80名志愿者,对其年龄进行统计后得到频率分布直方图如下,但是年龄组在[25,30)的数据不慎丢失. 在多面体ABCDE中,CD⊥平面ABC,BE∥CD,AB=2$\sqrt{5}$,AC=4,BC=2,CD=4,BE=1.
在多面体ABCDE中,CD⊥平面ABC,BE∥CD,AB=2$\sqrt{5}$,AC=4,BC=2,CD=4,BE=1. 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.