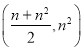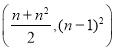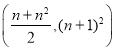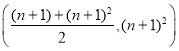题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对![]() a∈(0,1),是否存在实数λ,
a∈(0,1),是否存在实数λ,![]() ,使
,使![]() 成立,若存在,求λ的取值范围;若不存在,请说明理由.
成立,若存在,求λ的取值范围;若不存在,请说明理由.
【答案】(1)答案不唯一见解析(2)存在,![]() .
.
【解析】
(1)求函数导数,分![]() 三种情况,分析
三种情况,分析![]() 与
与![]() 的关系,即可求出函数的单调区间;
的关系,即可求出函数的单调区间;
(2)由题意转化为![]() 且
且![]() ,利用导数求出
,利用导数求出![]() ,
,![]() ,即转化为
,即转化为![]() ,构造函数
,构造函数![]() ,利用导数可求出
,利用导数可求出![]() ,即可求解.
,即可求解.
(1)![]()
![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①当a=0时,![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
②当a>0时,![]() ,
, ![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
③当a<0时,![]() ,
,
![]()
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,故当
,故当![]() 时,
时,![]()
当![]() 时,
时,![]() ,由(1)知,当
,由(1)知,当![]() 时,
时,![]()
所以![]() ,
,
若对![]() 使
使![]() 成立,即
成立,即![]()
则![]() 且
且![]() .
.
所以![]() ,所以
,所以 ![]() .
.
设![]() ,则
,则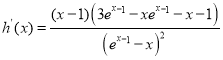 ,
,
令![]() 则
则![]() ,
,
当![]() 时,由
时,由![]() ,故
,故![]() ,
,
所以![]() ,故
,故![]() ,
,
所以![]() 在[0,1]上单调递减,
在[0,1]上单调递减,
所以![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() 时,
时, ![]() ,
,
所以当![]() 时,
时,![]() 单调递减,
单调递减,
所以当![]() 时,
时,![]() ,
,
即![]() 时,
时,![]() ,故
,故![]() .
.
所以当![]() 时,对
时,对![]()
使![]() 成立.
成立.

练习册系列答案
相关题目