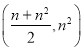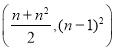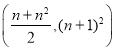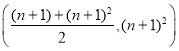题目内容
【题目】已知过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,点
,点![]() ,连接
,连接![]() 的直线与抛物线的另一交点分别为
的直线与抛物线的另一交点分别为![]() ,如图所示.
,如图所示.
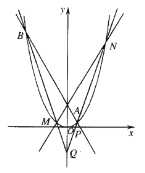
(Ⅰ)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(Ⅱ)试判断直线![]() 的斜率是否为定值,如果是,请求出此定值;如果不是,请说明理由.
的斜率是否为定值,如果是,请求出此定值;如果不是,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)是定值,定值为2
;(Ⅱ)是定值,定值为2
【解析】
(Ⅰ)首先根据条件设出直线![]() 的方程,然后联立抛物线方程,从而利用韦达定理求得直线
的方程,然后联立抛物线方程,从而利用韦达定理求得直线![]() 的斜率;
的斜率;
(Ⅱ)首先分别联立直线![]() 与抛物线的方程、直线
与抛物线的方程、直线![]() 与抛物线的方程,然后利用韦达定理求出
与抛物线的方程,然后利用韦达定理求出![]() ,
,![]() 的坐标,从而求得直线
的坐标,从而求得直线![]() 的斜率.
的斜率.
(Ⅰ)设点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则其方程为
,则其方程为![]() ,
,
与抛物线![]() 联立,得
联立,得![]() ,
,
所以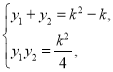 依题意
依题意![]() ,代入,得
,代入,得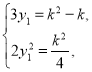 解得
解得![]() .
.
(Ⅱ)直线![]() 的斜率是定值.
的斜率是定值.
将直线![]() 与抛物线
与抛物线![]() 联立,得
联立,得![]() ,
,
所以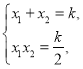 且
且![]() .
.
又因为直线![]() 的斜率为
的斜率为![]() ,其方程为
,其方程为![]() ,
,
与抛物线![]() 联立,得
联立,得![]() ,
,
故![]() ,即
,即![]() ,
,
所以点![]() 的坐标为
的坐标为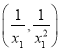 ,同理
,同理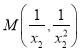 ,
,
所以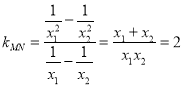 ,
,
即直线![]() 的斜率是定值.
的斜率是定值.

练习册系列答案
相关题目
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
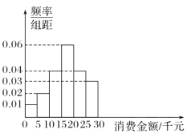
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |