题目内容
13.一根长l cm的线,一段固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系式是s=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$),其中g是重力加速度,当小球摆动的周期是1s时,线长l等于( )| A. | $\frac{g}{π}$ | B. | $\frac{g}{2π}$ | C. | $\frac{g}{{π}^{2}}$ | D. | $\frac{g}{{4π}^{2}}$ |
分析 由条件利用y=Acos(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,求得l的值.
解答 解:由s=s(t)=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$)的周期为1,可得 $\frac{2π}{\sqrt{\frac{g}{l}}}$=1,求得l=$\frac{g}{{4π}^{2}}$,
故选:D.
点评 本题主要考查余弦函数的周期性,利用了y=Acos(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
3.下列能与sin40°的值相等的是( )
| A. | cos40° | B. | sin(-40°) | C. | sin50° | D. | sin140° |
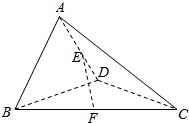 在四面体ABCD中,AC=BD,E,F分别为AD,BC的中点,且EF=$\frac{\sqrt{2}}{2}$AC,∠BDC=90°,求证:BD⊥平面ACD.
在四面体ABCD中,AC=BD,E,F分别为AD,BC的中点,且EF=$\frac{\sqrt{2}}{2}$AC,∠BDC=90°,求证:BD⊥平面ACD.