题目内容
8.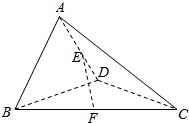 在四面体ABCD中,AC=BD,E,F分别为AD,BC的中点,且EF=$\frac{\sqrt{2}}{2}$AC,∠BDC=90°,求证:BD⊥平面ACD.
在四面体ABCD中,AC=BD,E,F分别为AD,BC的中点,且EF=$\frac{\sqrt{2}}{2}$AC,∠BDC=90°,求证:BD⊥平面ACD.
分析 作BC的中点G,连接EG,FG,先证明出EG⊥GF,进而证明出BD⊥EG,最后根据线面垂直的判定定理证明出BD⊥平面ACD.
解答 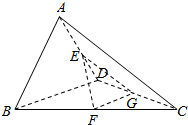 证明:作DC的中点G,连接EG,FG,
证明:作DC的中点G,连接EG,FG,
∴则EG=$\frac{1}{2}$AC=GF=$\frac{1}{2}$BD,EF=$\frac{\sqrt{2}}{2}$AC,
∴EG2+GF2=$\frac{1}{2}$AC2=EF2,
∴FG⊥FE,
∵EG∥AC,FG∥BD,∠BDC=90°,
∴BD⊥GE,BD⊥AC,
∵BD⊥DC,DC?平面ACD,AC?平面ACD,AC∪CD=C,
∴BD⊥平面ACD.
点评 本题主要考查了线面垂直的判定定理的应用,考查了空间想象能力和推论论证能力,证明的关键是找到两条相交的与之垂直的直线,属于中档题.

练习册系列答案
相关题目
9.设Sn是等差数列{an}的前n项和,若$\frac{S{\;}_{7}}{S{\;}_{14}}$=$\frac{2}{5}$,则$\frac{S{\;}_{14}}{S{\;}_{21}}$=( )
| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{9}$ |
3.直线y=kx+1与曲线y=ax3+lnx+b相切于点(1,5),则a-b=( )
| A. | -3 | B. | 2 | C. | 3 | D. | -2 |
13.一根长l cm的线,一段固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系式是s=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$),其中g是重力加速度,当小球摆动的周期是1s时,线长l等于( )
| A. | $\frac{g}{π}$ | B. | $\frac{g}{2π}$ | C. | $\frac{g}{{π}^{2}}$ | D. | $\frac{g}{{4π}^{2}}$ |
20.已知f(x)=$\left\{\begin{array}{l}{-x,x>0}\\{{x}^{2},x<0}\end{array}\right.$,则f[f(x)]=( )
| A. | $\left\{\begin{array}{l}{{x}^{2},x>0}\\{-{x}^{2},x<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{-{x}^{2},x>0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{-x,x>0}\\{{x}^{2},x<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{-x,x<0}\\{{x}^{2},x>0}\end{array}\right.$ |
18.设i为虚数单位,则复数2-i的模为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 1 |