题目内容
1.若方程|x2+4x+3|=x+4a有且仅有三个实数根,求实数a的值.分析 作出函数图象,写出抛物线x轴下方部分关于x轴对称的抛物线解析式,再与直线y=x+4a联立求出有一个交点时的a值,然后写出有3个解时的k值即可
解答 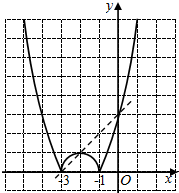 解:如图,x2+4x+3=(x+3)(x+1)=0,
解:如图,x2+4x+3=(x+3)(x+1)=0,
解得x1=-3,x2=-1,
所以抛物线y=(x+3)(x+1)与x轴的交点坐标为(-3,0),(-1,0),
x=-3时,-3+4a=0,解得a=$\frac{3}{4}$,
原抛物线x轴下方部分关于x轴对称的抛物线解析式为y=-(x+3)(x+1),
联立$\left\{\begin{array}{l}{y=-(x+3)(x+1)}\\{y=x+4a}\end{array}\right.$,
消掉y得,x2+5x+3+4a=0,
△=52-4×1×(3+4a)=0,
解得a=$\frac{13}{16}$,
所以方程有且仅有三个实数根时,a的值为$\frac{3}{4}$或$\frac{13}{16}$.
点评 本题考查了二次函数图象,一次函数图象,根据绝对值的性质要注意x轴下方部分的抛物线关于x轴对称,难点在于联立函数解析式求直线与抛物线关于x轴对称部分有一个交点时的情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.一根长l cm的线,一段固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系式是s=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$),其中g是重力加速度,当小球摆动的周期是1s时,线长l等于( )
| A. | $\frac{g}{π}$ | B. | $\frac{g}{2π}$ | C. | $\frac{g}{{π}^{2}}$ | D. | $\frac{g}{{4π}^{2}}$ |
10.已知a>0,b>0,a+b=1,(a+$\frac{1}{a}$)2+(b+$\frac{1}{b}$)2的最小值( )
| A. | 6 | B. | 8 | C. | 10 | D. | $\frac{25}{2}$ |