题目内容
【题目】已知函数f(x)=lnx﹣ax,a∈R.
(1)若f(x)有两个零点,求a的取值范围;
(2)设函数g(x)![]() ,证明:g(x)有极大值,且极大值小于
,证明:g(x)有极大值,且极大值小于![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由已知可得,![]() ,构造函数,转化为求解函数
,构造函数,转化为求解函数![]() 与
与![]() 的交点问题,结合函数的单调性即可求解.
的交点问题,结合函数的单调性即可求解.
(2)结合函数的导数与单调性的关系可证明![]() 的极值存在情况,然后结合函数的性质即可求解其范围.
的极值存在情况,然后结合函数的性质即可求解其范围.
(1)由f(x)=lnx﹣ax=0可得,a![]() ,
,
令h(x)![]() ,则h′(x)
,则h′(x)![]() ,
,
当x∈(0,e)时,h′(x)>0,h(x)单调递增,当x∈(e,+∞)时,h′(x)<0,h(x)单调递减,
∵h(e)![]() ,
,
x→0,h(x)→﹣∞,x→+∞,h(x)→0,
∴a![]() ;
;
(2)∵g(x)![]() ,
,
∴g′(x)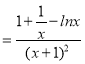 ,
,
令I(x)=1![]() ,则I(x)单调递减,
,则I(x)单调递减,
当x→0时,I(x)→+∞,当x→+∞时,I(x)→﹣∞,
∴I(x)一定存在变号的零点,g(x)存在极大值,
令I(x0)=1![]() 0,则g(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减,
0,则g(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减,
故极大值g(x0)![]() a
a![]() ,
,
又∵I(3)![]() ,
,
∴x0>3,又g(x0)![]() 在(0,+∞)上单调递减
在(0,+∞)上单调递减
∴g(x0)<![]()

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
