题目内容
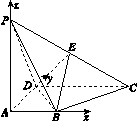
如图所示,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.

(1)求证:BE∥平面PAD;
(2)若BE⊥平面PCD,求平面EBD与平面BDC夹角的余弦值.

(1)求证:BE∥平面PAD;
(2)若BE⊥平面PCD,求平面EBD与平面BDC夹角的余弦值.
(1)见解析(2)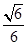
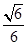
设AB=a,PA=b,如图所示,建立空间直角坐标系,则A(0,0,0),B(a,0,0),P(0,0,b),C(2a,2a,0),D(0,2a,0),E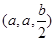 .
.
(1)证明: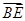 =
=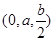 ,
,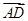 =(0,2a,0),
=(0,2a,0),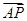 =(0,0,b),所以
=(0,0,b),所以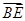 =
=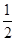
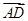 +
+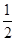
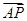 ,又BE?平面PAD,AD?平面PAD,AP?平面PAD,故BE∥平面PAD.
,又BE?平面PAD,AD?平面PAD,AP?平面PAD,故BE∥平面PAD.
(2)∵BE⊥平面PCD,∴BE⊥PC,即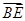 ·
·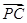 =0,
=0,
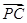 =(2a,2a,-b),∴
=(2a,2a,-b),∴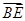 ·
·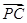 =2a2-
=2a2-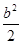 =0,即b=2a.
=0,即b=2a.
在平面BDE和平面BDC中,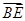 =(0,a,a),
=(0,a,a),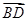 =(-a,2a,0),
=(-a,2a,0), =(a,2a,0),
=(a,2a,0),
所以平面BDE的一个法向量为n1=(2,1,-1),平面BDC的一个法向量为n2=(0,0,1).
cos〈n1,n2〉=-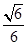 ,所以平面EBD与平面BDC夹角的余弦值为
,所以平面EBD与平面BDC夹角的余弦值为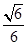 .
.
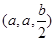 .
.
(1)证明:
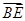 =
=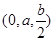 ,
,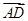 =(0,2a,0),
=(0,2a,0),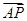 =(0,0,b),所以
=(0,0,b),所以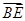 =
=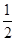
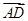 +
+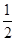
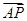 ,又BE?平面PAD,AD?平面PAD,AP?平面PAD,故BE∥平面PAD.
,又BE?平面PAD,AD?平面PAD,AP?平面PAD,故BE∥平面PAD.(2)∵BE⊥平面PCD,∴BE⊥PC,即
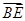 ·
·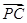 =0,
=0,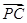 =(2a,2a,-b),∴
=(2a,2a,-b),∴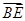 ·
·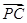 =2a2-
=2a2-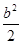 =0,即b=2a.
=0,即b=2a.在平面BDE和平面BDC中,
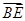 =(0,a,a),
=(0,a,a),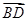 =(-a,2a,0),
=(-a,2a,0), =(a,2a,0),
=(a,2a,0),所以平面BDE的一个法向量为n1=(2,1,-1),平面BDC的一个法向量为n2=(0,0,1).
cos〈n1,n2〉=-
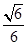 ,所以平面EBD与平面BDC夹角的余弦值为
,所以平面EBD与平面BDC夹角的余弦值为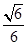 .
.
练习册系列答案
相关题目
 中,
中,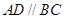 ,
,
 ,
, ,如图,把
,如图,把 沿
沿 翻折,使得平面
翻折,使得平面 平面
平面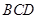 .
.


 ;
;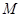 为线段
为线段 中点,求点
中点,求点 的距离;
的距离; ,使得
,使得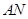 与平面
与平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.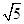 ,AB=AD=
,AB=AD=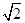 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).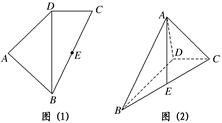
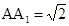 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.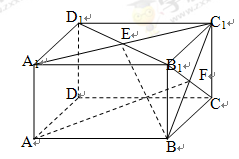
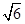 ,M是CC1的中点.
,M是CC1的中点.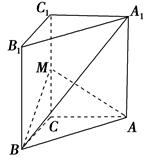
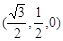 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
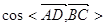 的值.
的值.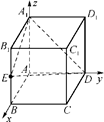
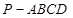 的底面是平行四边形,
的底面是平行四边形,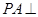 平面
平面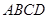 ,
,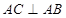 ,
,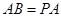 ,
,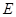 是
是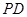 上的点,且
上的点,且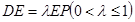 .
. 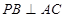 ;
;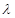 的值,使
的值,使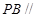 平面
平面 ;
;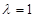 时,求三棱锥
时,求三棱锥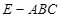 与四棱锥
与四棱锥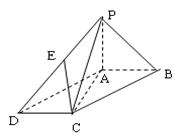
 )平行,则λ=( )
)平行,则λ=( )
