题目内容
已知数列{an}满足递推关系式:an+2an-an+12=tn(t-1),(n∈N*),且a1=1,a2=t.(t为常数,且t>1)
(1)求a3;
(2)求证:{an}满足关系式an+2-2tan+1+tan=0,(n∈N*;
(3)求证:an+1>an≥1(n∈N*).
解:(1)由a3a1-a22=t(t-1)和a1=1,a2=t
∴a3=2t2-t…(4分)
(2)由an+2an-an+12=tn(t-1),(n∈N*)
得an+1an-1-an2=tn-1(t-1)(n≥2),
再由上两式相除得到:∴an+2an-an+12=tan+1an-1-tan2
∴an(an+2+tan)=an+1(an+1+tan-1)
∴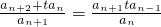
即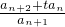 为常数列
为常数列
∴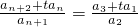
而a3+ta1=2t2∴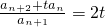 .
.
即an+2-2tan+1+tan=0.…(9分)
(3)由t>1知:an+2an>an+12≥0
∴an+2an>0
故an+2与an同号
而a1=1>0,a2=t>0.
故an>0.
又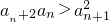
即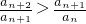
∴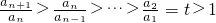
∴an+1>an
∴an≥1
∴an+1>an≥1.…(14分)
分析:(1)由a3a1-a22=t(t-1)和a1=1,a2=t,能求出a3.
(2)由an+2an-an+12=tn(t-1),(n∈N*)得an+1an-1-an2=tn-1(t-1)(n≥2),所以an+2an-an+12=tan+1an-1-tan2,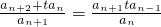 ,由此能够证明an+2-2tan+1+tan=0.
,由此能够证明an+2-2tan+1+tan=0.
(3)由t>1知:an+2an>an+12≥0,所以an+2an>0,故an+2与an同号,由此能够证明an+1>an≥1.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意不等式性质的合理运用.
∴a3=2t2-t…(4分)
(2)由an+2an-an+12=tn(t-1),(n∈N*)
得an+1an-1-an2=tn-1(t-1)(n≥2),
再由上两式相除得到:∴an+2an-an+12=tan+1an-1-tan2
∴an(an+2+tan)=an+1(an+1+tan-1)
∴
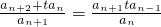
即
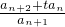 为常数列
为常数列∴
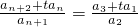
而a3+ta1=2t2∴
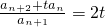 .
.即an+2-2tan+1+tan=0.…(9分)
(3)由t>1知:an+2an>an+12≥0
∴an+2an>0
故an+2与an同号
而a1=1>0,a2=t>0.
故an>0.
又
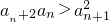
即
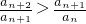
∴
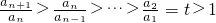
∴an+1>an
∴an≥1
∴an+1>an≥1.…(14分)
分析:(1)由a3a1-a22=t(t-1)和a1=1,a2=t,能求出a3.
(2)由an+2an-an+12=tn(t-1),(n∈N*)得an+1an-1-an2=tn-1(t-1)(n≥2),所以an+2an-an+12=tan+1an-1-tan2,
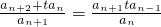 ,由此能够证明an+2-2tan+1+tan=0.
,由此能够证明an+2-2tan+1+tan=0.(3)由t>1知:an+2an>an+12≥0,所以an+2an>0,故an+2与an同号,由此能够证明an+1>an≥1.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意不等式性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目