题目内容
【题目】已知函数 ,若存在实数
,若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根,则实数
有两个不同的实根,则实数![]() 的取值范围是()
的取值范围是()
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
【答案】C
【解析】
若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根,等价于存在实数k,使函数
有两个不同的实根,等价于存在实数k,使函数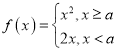 与函数
与函数![]() 的图象有两个不同的交点,然后对
的图象有两个不同的交点,然后对![]() 分四种情况讨论,作出函数
分四种情况讨论,作出函数![]() 的图象,根据图象可以得到实数
的图象,根据图象可以得到实数![]() 的范围.
的范围.
联立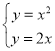 ,解得
,解得![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
如图:
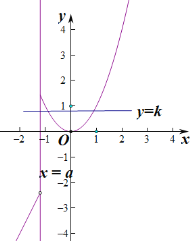
由图可知,存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
当![]() 时,函数
时,函数![]() 在R上递增,
在R上递增,
如图:
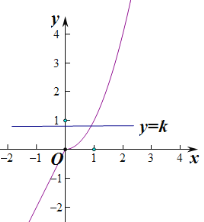
由图可知,不存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上也递增,并且
上也递增,并且![]() ,
,
如图:
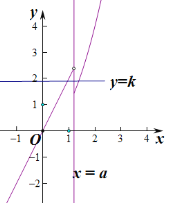
由图可知, 存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根;
有两个不同的实根;
当![]() 时,
时,![]() 在R上是增函数,
在R上是增函数,
如图:
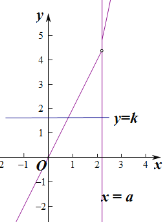
由图可知,不存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有两个不同的实根.
有两个不同的实根.
综上所述: 实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
故选C.

练习册系列答案
相关题目
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。