题目内容
如图,已知椭圆
+
=1(a>b>0)的右焦点为F(c,0),下顶点为A(0,-b),直线AF与椭圆的右准线交于点B,与椭圆的另一个交点为点C,若F恰好为线段AB的中点.
(1)求椭圆的离心率;
(2)若FC=
,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的离心率;
(2)若FC=
| 2 |
| 3 |
分析:(1)依题意,可求得2c=
,从而可求得椭圆的离心率;
(2)由(1)可知直线AB的方程为y=x-c,设C(x0,x0-c),将其代入椭圆方程,可求得x0,利用两点间的距离公式表示出FC=
,可求得c,从而可求得椭圆的方程.
| a2 |
| c |
(2)由(1)可知直线AB的方程为y=x-c,设C(x0,x0-c),将其代入椭圆方程,可求得x0,利用两点间的距离公式表示出FC=
| 2 |
| 3 |
解答:解(1)因为B在右准线上,且F恰好为线段AB的中点,所以2c=
,…(2分)
即
=
,所以椭圆的离心率e=
…(4分)
(2)由(1)知a=
c,b=c,所以直线AB的方程为y=x-c,
设C(x0,x0-c),因为点C在椭圆上,所以
+
=1,…(6分)
即x02+2(x0-c)2=2c2,
解得x0=0(舍去),x0=
c.
所以C为(
c,
c),…(8分)
因为FC=
,由两点距离公式可得(
c-c)2+(
c)2=
,
解得c2=2,所以a=2,b=
,
所以此椭圆的方程为
+
=1. …(10分)
| a2 |
| c |
即
| c2 |
| a2 |
| 1 |
| 2 |
| ||
| 2 |
(2)由(1)知a=
| 2 |
设C(x0,x0-c),因为点C在椭圆上,所以
| x02 |
| 2c2 |
| (x0-c)2 |
| c2 |
即x02+2(x0-c)2=2c2,
解得x0=0(舍去),x0=
| 4 |
| 3 |
所以C为(
| 4 |
| 3 |
| 1 |
| 3 |
因为FC=
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
解得c2=2,所以a=2,b=
| 2 |
所以此椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
点评:本题考查椭圆的简单性质(求离心率),考查椭圆的标准方程,着重考查方程思想与化归思想的综合应用,属于中档题.

练习册系列答案
相关题目
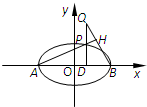 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆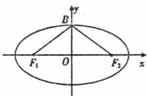 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆