题目内容

2．已知异面直线a，b成60°角，A为空间中一点，则过A与a，b都成45°角的平面（　　）
A．有且只有一个B．有且只有两个C．有且只有三个D．有且只有四个

分析 已知平面过A，再知道它的方向，就可以确定该平面了，因为涉及到平面的方向，我们考虑它的法线，并且假设a，b为相交直线也没关系，于是原题简化为：已知两条相交直线a，b成60°角，求空间与a，b都成45°角的直线．

解答 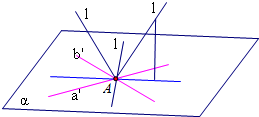解：已知平面过A，再知道它的方向，就可以确定该平面了
∵涉及到平面的方向，我们考虑它的法线，并且假设a，b为相交直线也没关系，
∴原题简化为：已知两条相交直线a，b成60°角，求空间与a，b都成45°角的直线．
过P作a′∥a，b′∥b，设直线a′、b′确定的平面为α，
∵异面直线a、b成60°角，∴直线a′、b′确所成锐角为60°
①当直线l在平面α内时，若直线l平分直线a′、b′确所成的钝角，
则直线l与a、b都成60°角，不成立；
②当直线l与平面α斜交时，若它在平面α内的射影恰好落在
直线a′、b′确所成的锐角平分线上时，直线l与a、b所成角相等．
此时l与a'、b'所成角的范围为[30°，90°]，
适当调整l的位置，可使直线l与a、b也都成45°角，这样的直线l有两条．
综上所述，过点P与a′、b′确都成45°角的直线，可以作2条．
∴过A与a，b都成45°角的平面有且只有2个．
故选：B．

点评 本题考查满足条件的平面个数的求法，是中档题，解题时要认真审题，注意等价转化思想的合理运用．

练习册系列答案
相关题目
12．已知A（-$\frac{2}{{k}^{2}-1}$，0），B（0，-$\frac{2k}{{k}^{2}-1}$），其中k≠0且k≠±1，直线l经过点P（1，0）和AB的中点．
（1）求证：A，B关于直线l对称；
（2）当1＜k＜$\sqrt{2}$时，求直线l在y轴上的截距b的取值范围．
13．已知a∈R+，b∈[-2，$\sqrt{2}$]，则u=（b-a）2+（$\sqrt{2-{b}^{2}}$-$\frac{9}{a}$）2的最小值为8．
10．已知f（x）=$\left\{\begin{array}{l}{-2（x-\frac{1}{2}）^{2}+1\\;x∈[0，\frac{1}{2}）}\\{-2x+2\\;x∈[\frac{1}{2}，1]}\end{array}\right.$，求函数y=f[f（x）]-x的所有零点之和．
17．已知（2-$\sqrt{3}$x）3=a0+a1x+a2x2+a3x3，则（a0+a2）2-（a1+a3）2=1．
7．有专业机构认为甲型H7N9禽流感在一段时间没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过15人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（　　）
A．甲地：总体均值为6，中位数为8B．乙地：总体均值为5，方差为12
C．丙地：中位数为5，众数为6D．丁地：总体均值为3，方差大于0
14．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，过右焦点F的直线l与C相交于A、B两点，当l的斜率为1时，坐标原点O到l的距离为1．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$成立？若存在，求出所有的P的坐标与l的方程；若不存在，说明理由．
11．如图，已知AB⊥平面BCE，CD∥AB，△BCE是等腰直角三角形，其中∠EBC=$\frac{π}{2}$，且AB=BC=2CD=2．
（1）在线段BE上是否存在一点F，使CF∥平面ADE？
（2）求线段AB上是否存在点M，使得点B到面CEM的距离等于1？如果不存在，请说明理由由．
12．已知恒等式$\frac{sinα}{1+cosα}$=$\frac{1-cosα}{sinα}$就是平方关系sin2α+cos2α=1的一种变形，请你写出利用同角三角函数基本关系的变形而导出的一个恒等式：$\frac{1+sinα}{cosα}=\frac{cosα}{1-sinα}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网