Question

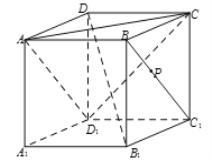
【题目】如图所示的几何体 为一简单组合体，在底面 中， ， ， ， 平面 ， ， ， ．

（1）求证：平面 平面 ；
（2）求该组合体 的体积．

Answer 1

【答案】
（1）证明：因为 平面 ， ，所以 平面 ，
又因为 平面 ，所以 ，又因为 ，且 ，
所以 平面 ，又因为 平面 ，所以平面 平面
（2）解：面 将几何体分成四棱锥 和三棱锥 两部分，
过 作 ，因为 平面 ， 平面 ，
所以 ，又因为 ， ，
所以 平面 ，即 为四棱锥 的高，
并且 ， ，所以 ，
因为 平面 ，且已知 ，
△ 为顶角等于 的等腰三角形， ， ，
所以 ，
所以组合体 的体积为 ．
【解析】(1)根据题意借助题设条件运用平面与平面垂直的判定定理即可得出结论。(2)根据题设条件将几何体分割成四棱锥和三棱锥再分别求出其体积进而可得出所求的几何体的体积。