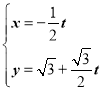题目内容
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
表1
停车距离 |
|
|
|
|
|
频数 | 24 | 42 | 24 | 9 | 1 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
(附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为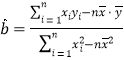 ,
,![]() )
)
【答案】(1)27.1(2)![]() (3)大于
(3)大于![]() 毫克时为“醉驾”
毫克时为“醉驾”
【解析】分析:(1)每个区间的中点作为估计值进行计算可得平均数;
(2)根据所给公式计算回归方程中的系数即可;
(3)由(2)解不等式![]() 可得.
可得.
详解:(1)![]()
(2)![]()
![]()
∴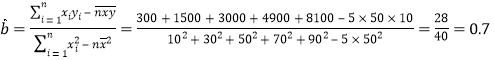
![]()
∴回归方程为![]()
(3)由题意知:![]() ,∴
,∴![]()
∴预测当每毫升血液酒精含量大于![]() 毫克时为“醉驾”
毫克时为“醉驾”

练习册系列答案
相关题目
【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|