题目内容
(本题满分16分)
在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切于坐标原点
相切于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点
到椭圆右焦点![]() 的距离等于线段
的距离等于线段![]() 的长.若存在,请求出点
的长.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解析:(1)设圆C的圆心为(m, n)(m<0,n>0),依题意有 解得
解得![]()
所求的圆的方程为![]() …………6分
…………6分
(2)由已知可得![]() ∴
∴![]() …………8分
…………8分
∴椭圆的方程为![]() ,右焦点为F(4, 0); …………10分
,右焦点为F(4, 0); …………10分
从而以F为圆心,FO为半径的圆的方程为(x 4) 2 + y 2 = 16; …………12分
又CF=2![]() <4 + 2
<4 + 2![]() ,所以圆F与圆C交于两个不同的点;
,所以圆F与圆C交于两个不同的点;
所以圆C上存在异于原点的点Q,使Q到椭圆右焦点F的距离等于线段OF的长,
易知点Q与原点关于CF对称,所以O关于CF:x + 3y 4=0的对称点为Q(x0, y0)
则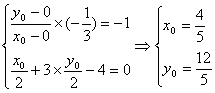 ,所以Q点的坐标为
,所以Q点的坐标为![]() .…………16分
.…………16分
w.w.w.k.s.5.u.c.o.m

练习册系列答案
相关题目

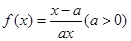
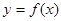 在
在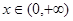 上的单调性;
上的单调性;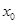 ,使
,使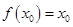 ,则称
,则称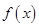 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求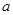 的值;
的值;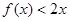 在
在