题目内容
(本小题满分12分)
 函数
函数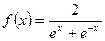 .
.
(Ⅰ) 判断函数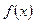 的奇偶性,并求其最大值;
的奇偶性,并求其最大值;
(Ⅱ) 求证: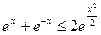 ;
;
(Ⅲ) 求证: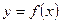 的图象
的图象 与
与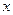 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于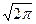 .
.
 函数
函数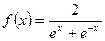 .
.(Ⅰ) 判断函数
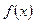 的奇偶性,并求其最大值;
的奇偶性,并求其最大值;(Ⅱ) 求证:
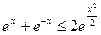 ;
;(Ⅲ) 求证:
 的图象
的图象 与
与 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于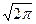 .
.(Ⅰ)偶函数,最大值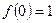
(Ⅱ)证明见解析
(Ⅲ)证明见解析
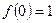
(Ⅱ)证明见解析
(Ⅲ)证明见解析
(Ⅰ)定义域为
 ,
,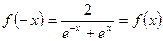 ,则
,则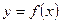 为偶函数,
为偶函数,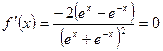 ,则
,则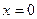 ,
,所以函数
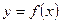 在
在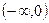 上单调递增,在
上单调递增,在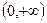 上单调递减,
上单调递减,则最大值
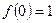 ;------------------------------------------------------
;------------------------------------------------------ 4分
4分(Ⅱ)要证明
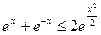 ,
,只
 需证
需证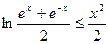 ,
,设

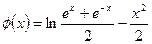 ,
,则
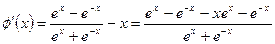
令
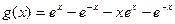
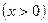 ,则
,则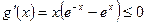
所以,
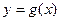 在
在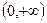 上为单调递减函数,
上为单调递减函数,因此,

所以当
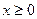 时,
时,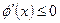 ,又因为
,又因为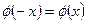 ,则
,则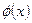 为偶函数,
为偶函数,所以
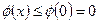 ,则原结论成立;-
,则原结论成立;- ---------------------------------------8分
---------------------------------------8分(Ⅲ)由标准正态分布
 与
与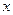 轴围成的面积为
轴围成的面积为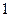 ,
,则由(Ⅱ)得
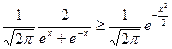 ,
,则
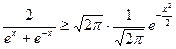 ,
,所以
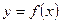 的图象与
的图象与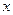 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于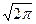 .------------------12分
.------------------12分
练习册系列答案
相关题目
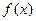 =
=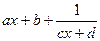 (
(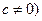 的对称中心为
的对称中心为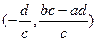
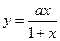 的图像关于直线
的图像关于直线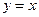 对称,则
对称,则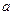 为
为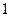
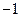
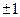
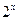 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=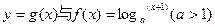 的图象关于原点对称.
的图象关于原点对称.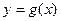 的解析式;
的解析式;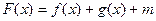 为奇函数,试确定实数m的值;
为奇函数,试确定实数m的值;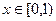 时,总有
时,总有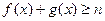 成立,求实数n的取值范围.
成立,求实数n的取值范围.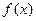 为定义在R上的奇函数,当
为定义在R上的奇函数,当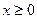 时,
时,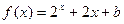 (b为常数),则
(b为常数),则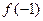 =
=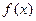 是定义在区间
是定义在区间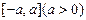 上的奇函数,若
上的奇函数,若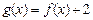 ,则
,则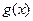 的最大值与最小值之和为 .
的最大值与最小值之和为 .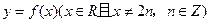 是周期为4的函数,
是周期为4的函数,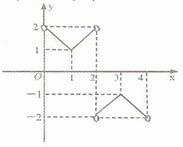
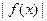 的值域是
的值域是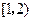 ;③关于
;③关于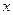 的方程
的方程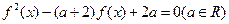 必有实根;
必有实根;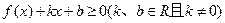 的解集非空。其中正确命题的个数为( ▲ )
的解集非空。其中正确命题的个数为( ▲ )