袋中有6个红球.4个白球.从袋中任取4个球.则至少有2个白球的概率是( )A．$\frac{23}{42}$B．$\frac{1}{7}$C．$\frac{17}{42}$D．$\frac{5}{42}$ 题目和参考答案——青夏教育精英家教网—

题目内容

7．袋中有6个红球、4个白球，从袋中任取4个球，则至少有2个白球的概率是（　　）

A．

$\frac{23}{42}$

B．

$\frac{1}{7}$

C．

$\frac{17}{42}$

D．

$\frac{5}{42}$

分析先计算出从袋中任取4个球的方法总数，再计算至少有2个白球的方法数，代入古典概型概型计算公式，可得答案．

解答解：根据题意，首先分析从6个红球、4个白球中任取4个球，共C₁₀⁴=210种取法，
其中至少有2个白球有${C}_{4}^{2}{C}_{6}^{2}$+${C}_{4}^{3}{C}_{6}^{1}$+${C}_{4}^{4}$=115，
故从袋中任取4个球，则至少有2个白球的概率P=$\frac{115}{210}$=$\frac{23}{42}$，
故选：A．

点评本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．

练习册系列答案

18．${∫}_{0}^{1}$（e^x+2x）dx等于（　　）

$\frac{{\sqrt{6}-\sqrt{2}}}{4}$

B．

$\frac{{\sqrt{6}+\sqrt{2}}}{4}$

2．定义在R上的函数g（x）及二次函数h（x）满足：g（x）+2g（-x）=e^x+$\frac{2}{ex}$-9，h（-2）=h（0）=1且h（-3）=-2．
（1）求g（x）和h（x）的解析式；
（2）对于x₁，x₂∈[-1，1]，均有h（x₁）+ax₁+5≥g（x₂）-x₂g（x₂）成立，求a的取值范围．

12．已知函数f（x）=x²-2a²lnx（a＞0）．
（1）若f（x）在x=1处取得极值，求实数a的值；
（2）求函数f（x）的单调区间．

19．（文）已知数列{a_n}的前n项和为S_n=n²+$\frac{1}{2}$n，则数列的通项公式a_n=$2n-\frac{1}{2}$；
（理）已知数列{a_n}的前n项和为S_n=$\frac{1}{4}{n^2}+\frac{2}{3}$n+3，则数列的通项公式a_n=$\left\{\begin{array}{l}{\frac{47}{12}，}&{n=1}\\{\frac{6n+5}{12}，}&{n≥2}\end{array}\right.$．

16．

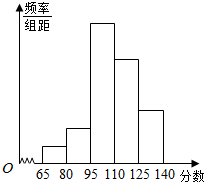为了解某校高三学生质检数学成绩分布，从该校参加质检的学生数学成绩中抽取一个样本，并分成5组，绘成如图所示的频率分布直方图．若第一组至第五组数据的频率之比为1：2：8：6：3，最后一组数据的频数是6．用频率估计概率的方法，估计该校高三学生质检数学成绩在125～140分之间的概率和样本容量为（　　）

	A．	?x₀∈R，${e^{x_0}}$＜0
	B．	函数$f（x）={x^2}-{log_{\frac{1}{2}}}$x的零点个数为2
	C．	若p∨q为真命题，则p∧q也为真命题
	D．	命题“若m＞0，则方程x²+x-m=0有实数根”的逆否命题为：“若方程x²+x-m=0无实数根，则m≤0”

试题分类