题目内容
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)=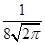 .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
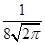 .
.(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
(1) 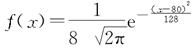 (2) 68.26%
(2) 68.26%
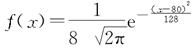 (2) 68.26%
(2) 68.26%解:(1)由于正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,
所以正态曲线关于直线x=80对称,且在x=80处取得最大值.
因此得μ=80,
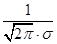 =
=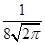 ,所以σ=8.
,所以σ=8.故正态分布密度函数的解析式是
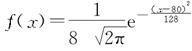
(2)由μ=80,σ=8,得
μ-σ=80-8=72,μ+σ=80+8=88,
所以零件尺寸X在区间(72,88)内的概率是0.6826.因此尺寸在72mm~88mm间的零件大约占总数的68.26%.

练习册系列答案
相关题目
 )则使P(η=k)最大的k是( )
)则使P(η=k)最大的k是( )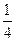
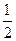

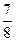
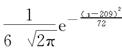 ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.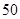 名学生,一次考试的数学成绩
名学生,一次考试的数学成绩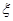 服从正态分布
服从正态分布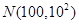 ,已知
,已知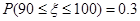 ,估计该班学生成绩在
,估计该班学生成绩在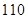 以上的人数为 人。
以上的人数为 人。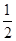 ,则μ= ( ).
,则μ= ( ).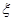 服从正态分布
服从正态分布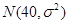 ,若
,若 ,则
,则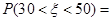 ( )
( )
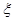 服从正态分布
服从正态分布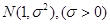 ,若
,若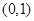 内取值的概率为
内取值的概率为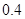 ,则
,则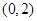 内取值的概率为 。
内取值的概率为 。