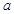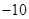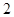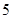题目内容
(本小题满分12分)
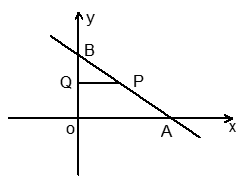
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点. 且PQ∥OA交OB于点Q.
(1)若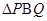 和四边形
和四边形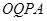 的面积满足
的面积满足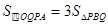 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;
(2)在x轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点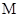 与
与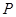 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点. 且PQ∥OA交OB于点Q.

(1)若
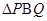 和四边形
和四边形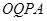 的面积满足
的面积满足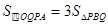 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;(2)在x轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点
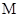 与
与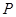 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.(1)P为AB的中点,PQ=4;(2)点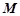 、
、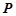 的坐标分别为(0,0),(
的坐标分别为(0,0),(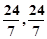 );或者点
);或者点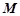 、
、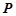 的坐标分别为(
的坐标分别为(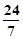 ,0),(
,0),(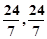 );或者点
);或者点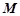 、
、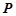 的坐标分别为(
的坐标分别为(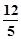 ,0),(
,0),(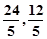 )。
)。
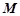 、
、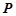 的坐标分别为(0,0),(
的坐标分别为(0,0),(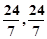 );或者点
);或者点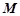 、
、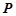 的坐标分别为(
的坐标分别为(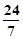 ,0),(
,0),(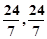 );或者点
);或者点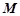 、
、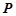 的坐标分别为(
的坐标分别为(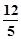 ,0),(
,0),(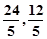 )。
)。试题分析:(1)
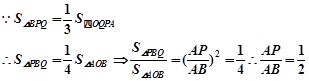
 即P为AB的中点, ∴PQ=
即P为AB的中点, ∴PQ=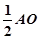 ="4" .--------------------------4分
="4" .--------------------------4分(2)由已知得l方程为3x+4y="24" (*)
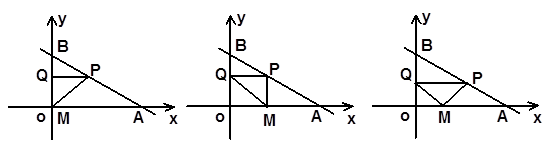
①当∠PQM=90°时,由PQ∥OA且|PQ|=|MQ|此时M点与原点O重合,设Q(0,a)则
 P(a,a)
P(a,a)有(a,a)代入(*)式得a=
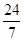 .
.点
 、
、 的坐标分别为(0,0),(
的坐标分别为(0,0),(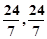 )----------------------6分
)----------------------6分②当∠MPQ=90°,由PQ∥OA 且|MP|=|PQ|设Q(0,a,)则M(0, a), P(a,a)进而得
 a=
a=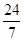
∴点
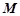 、
、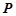 的坐标分别为(
的坐标分别为(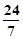 ,0),(
,0),(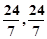 )----------------------8分
)----------------------8分③当∠PMQ=90°,由PQ∥OA,|PM|=|MQ|且|OM|=|OQ|=
 |PQ|
|PQ|
设Q(0,a,)则M(a,0)点P坐标为(2a,a)代入(*)式 得a=
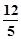 .
.∴点
 、
、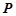 的坐标分别为(
的坐标分别为(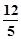 ,0),(
,0),(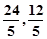 )----------------------12分
)----------------------12分点评:学生做此题的第二问时,一定要认真审题,注意分类讨论思想的应用。要满足∆PQM为直角三角形,需要讨论三个内角分别为直角的情况。

练习册系列答案
相关题目
 中,已知射线
中,已知射线 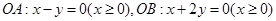 ,过点
,过点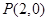 作直线分别交射线
作直线分别交射线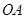 、
、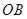 于点
于点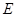 、
、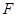 ,若
,若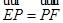 ,则直线
,则直线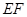 的斜率为
的斜率为 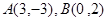 则直线
则直线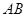 的方程是_____________
的方程是_____________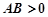 ,
,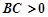 ,那么直线
,那么直线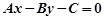 不经过的象限是 ( )
不经过的象限是 ( )
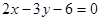 在
在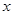 轴上的截距为
轴上的截距为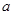 ,在
,在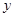 轴上的截距为
轴上的截距为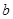 ,则( )
,则( )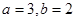
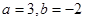
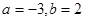
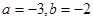
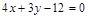 的距离为 .
的距离为 . 、
、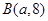 两点的直线与直线
两点的直线与直线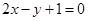 平行,则
平行,则