题目内容
14.已知数列{an}的前n项和为Sn,且Sn=2an-n;(1)求证:数列{an+1}为等比数列;
(2)令bn=anlog2(an+1),求数列{bn}的前n项和.
分析 (1)由Sn=2an-n,可得Sn-1=2an-1-(n-1),两式相减可得an+1=2(an-1+1),故数列{an+1}为等比数列,由此可求;
(2)由(1)可得bn=anlog2(an+1)=n(2n-1),然后分两部分求和,一部分错位相减,一部分等差数列的求和公式,即可得答案.
解答 解:(1)证明:n=1时,a1=S1=2a1-1,解得a1=1;
∵Sn=2an-n,∴Sn-1=2an-1-(n-1),
∴an=2an-2an-1-1,从而an=2an-1+1,
即an+1=2(an-1+1),
∴数列{an+1}为等比数列,
因此an+1=(a1+1)•2n-1,
∴an=2n-1;
(2)由(1)可得bn=anlog2(an+1)
=n(2n-1),
记An=1•2+2•22+3•23+…+n•2n,①
2An=1•22+2•23+3•24+…+n•2n+1,②
①-②,得:-An=2+22+23+…+2n-n•2n+1
=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1,
∴An=(n-1)•2n+1+2,
∴Tn=(n-1)•2n+1+2+$\frac{n(n+1)}{2}$.
点评 本题为数列的综合应用,涉及错位相减法求和以及分项求和,属中档题.

练习册系列答案
相关题目
4.下列计算正确的是( )
| A. | xm•x3=x3m | B. | (-4a3)2=4a6 | C. | (-x2)3=-x6 | D. | -(-m2)4=m8 |
9.已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)>0,则函数f(x)在(a,b)内( )
| A. | 肯定没有零点 | B. | 至多有一个零点 | ||
| C. | 可能有两个零点 | D. | 以上说法均不正确 |
12.如果cos(π-A)=-$\frac{1}{2}$,那么cosA的值为( )
| A. | --$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
9.设集合A={x|x≤1},B={x|x>p},要使A∩B=∅,则p应满足的条件是( )
| A. | p<1 | B. | p≤1 | C. | p>1 | D. | p≥1 |
10.已知集合A={x|y=lnx},集合B={-2,-1,1,2},则A∩B=( )
| A. | (0,+∞) | B. | {-1,-2} | C. | (1,2) | D. | {1,2} |
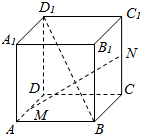 如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.
如图所示,在正方体ABCD一A1B1C1D1中,取$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$作为基底.