题目内容
本小题满分12分)已知函数f(x)=ax3+mx2-m2x+1(m<0)在点x=-m处取得极值.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间.
解:(Ⅰ)f′(x)=3ax2+2mx-m2 ∵函数f(x)在点x=-m处取得极值.
f′(-m)=0 ∴3am2-2m2-m2=0∴a=1,经检验,a=1满足题意 ------5分
(Ⅱ)由(Ⅰ)可知,f(x)=x3+mx2-m2x+1,所以f′(x)=3x2+2mx-m2=(x+m)(3x-m)(m<0)
令f′(x)>0,解得
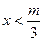 或
或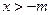 ,令f′(x)<0,解得
,令f′(x)<0,解得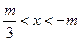
所以,函数f(x)的单调递增区间为,(-m,+∞);
单调递减区间为(,-m) ------ 12分
略

练习册系列答案
相关题目
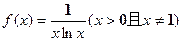
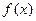 的单调区间;
的单调区间;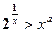 对任意
对任意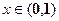 恒成立,求实数
恒成立,求实数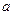 的取值范围.
的取值范围.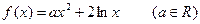 ,设曲线
,设曲线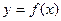 在点
在点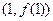 处的切线为
处的切线为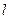 ,若
,若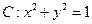 相切,求
相切,求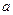 的值.
的值.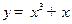 的递增区间是( )
的递增区间是( ) B
B 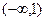 C
C 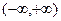 D
D 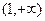
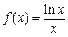 ,在区间[2,3]上任取一点
,在区间[2,3]上任取一点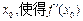 >0的概率为
>0的概率为  。
。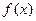 在
在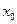 处的导数存在,则
处的导数存在,则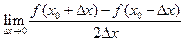 等于 ( )
等于 ( ) 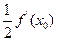
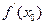
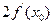
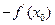
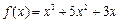 在区间
在区间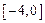 上的最大值是 .
上的最大值是 .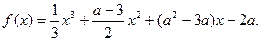
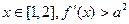 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;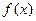 的两个极
的两个极 值点分别为
值点分别为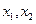 判断①
判断①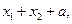 ②
②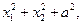 ③
③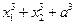 是否为定值?若是定值请求出;若不是定值,请把不是定
是否为定值?若是定值请求出;若不是定值,请把不是定 值的表示为函数
值的表示为函数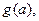 并求出
并求出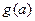 的最小值;
的最小值;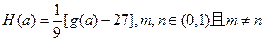 ,试比较
,试比较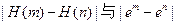 (e为自然对数的底)的大小,并证明。
(e为自然对数的底)的大小,并证明。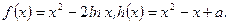
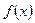 的极值;
的极值;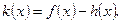 若函数
若函数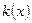 在
在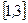 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 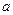 的取值范围.
的取值范围.